Thevenins teorem uttaler at det er mulig å forenkle enhver lineær krets, uansett hvor kompleks, til en ekvivalent krets med bare en enkelt spenningskilde og seriemotstand koblet til en belastning. Kvalifiseringen av «lineær» er identisk med den som finnes i Superposisjonssetningen, der alle underliggende ligninger må være lineære (ingen eksponenter eller røtter). Hvis vi har å gjøre med passive komponenter (for eksempel motstander og senere, induktorer og kondensatorer) Det er sant. Imidlertid er det noen komponenter (spesielt visse gassutladnings- og halvlederkomponenter) som er ikke-lineære: det vil si at deres motstand mot strømendringer med spenning og / eller strøm. Som sådan vil vi kalle kretser som inneholder disse typer komponenter, ikke-lineære kretser.
Thevenins teorem i kraftsystemer
Thevenins teorem er spesielt nyttig for å analysere kraftsystemer og andre kretser der en bestemt motstand i kretsen (kalt «belastning ”Motstand) kan endres, og ny beregning av kretsen er nødvendig med hver prøveverdi av belastningsmotstand, for å bestemme spenningen over den og strømmen gjennom den. La oss ta en titt på eksemplets krets:

La oss anta at vi bestemmer oss for å betegne R2 som «last» -motstanden i Denne kretsen. Vi har allerede fire analysemetoder til rådighet (grenstrøm, nettstrøm, Millmans teorem og superposisjonssetning) for å bestemme spenningen over R2 og strøm gjennom R2, men hver av disse metodene er tidkrevende. Tenk deg å gjenta noen av disse metodene om og om igjen for å finne ut hva som ville skje hvis lastmotstanden endret seg (endring av lastmotstand er veldig vanlig i kraftsystemer, da flere belastninger slås på og av etter behov. Den totale motstanden til deres parallelle tilkoblinger endres. avhengig av hvor mange som er tilkoblet om gangen. Dette kan potensielt innebære mye arbeid!
Thevenin Equivalent Circuit
Thevenins teorem gjør dette enkelt ved midlertidig å fjerne lastmotstanden fra original krets og redusere det som er igjen til en tilsvarende cir kappe sammensatt av en enkelt spenningskilde og seriemotstand. Lastmotstanden kan deretter kobles til denne «Thevenin-ekvivalente kretsen» og beregninger utføres som om hele nettverket ikke var noe annet enn en enkel seriekrets:

… etter Thevenin-konvertering..
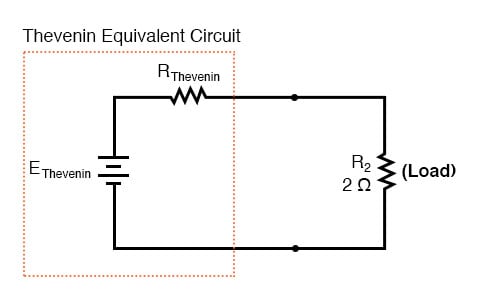
«Thevenin Equivalent Circuit» er den elektriske ekvivalenten til B1, R1, R3 og B2 sett fra de to punktene der belastningsmotstanden (R2) kobles til.
Thevenin-ekvivalent krets, hvis den er riktig avledet, vil oppføre seg nøyaktig det samme som den opprinnelige kretsen dannet av B1, R1, R3 og B2. Med andre ord skal belastningsmotstanden (R2) spenning og strøm være nøyaktig den samme for den samme verdien av lastmotstand i de to kretsene. Lastmotstanden R2 kan ikke «fortelle forskjellen» mellom det opprinnelige nettverket av B1, R1, R3 og B2, og Thevenin-ekvivalente kretsen til EThevenin og RThevenin, forutsatt at verdiene for EThevenin og RThevenin er beregnet riktig.
Fordelen ved å utføre «Thevenin-konverteringen» til den enklere kretsen er selvfølgelig at den gjør belastningsspenning og laststrøm så mye lettere å løse enn i det opprinnelige nettverket. Å beregne ekvivalent Thevenin-kildespenning og seriemotstand er faktisk ganske enkelt. Først blir den valgte lastemotstanden fjernet fra den opprinnelige kretsen, erstattet med en pause (åpen krets):

Bestem Thevenin Spenning
Deretter bestemmes spenningen mellom de to punktene der lastemotstanden pleide å være festet. Bruk de analysemetodene som står til din disposisjon for å gjøre dette. I dette tilfellet er den opprinnelige kretsen med lastmotstanden fjernet ikke noe mer enn en enkel seriekrets med motsatte batterier, og slik kan vi bestemme spenningen over de åpne belastningsterminalene ved å bruke reglene for seriekretser, Ohms lov og Kirchhoffs spenning Lov:

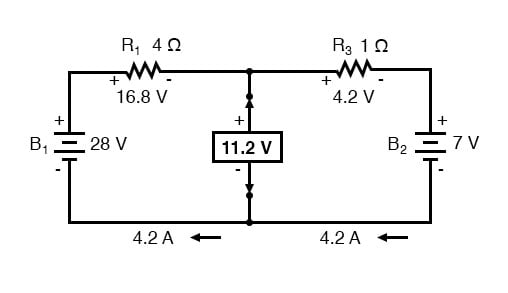
Spenningen mellom de to lasttilkoblingspunktene kan regnes ut fra en av batteriets spenninger, og en av motstandens spenning faller og blir 11,2 volt.Dette er vår «Theveninspenning» (EThevenin) i ekvivalent krets:

Bestem Thevenin Series Resistance
For å finne motstanden fra Thevenin-serien for vår tilsvarende krets, må vi ta den originale kretsen (med lastmotstanden fortsatt fjernet), fjerne strømkildene (i samme stil som vi gjorde med Superposisjonssetningen: spenningskilder erstattet med ledninger og strømkilder erstattet med brudd), og figurer motstanden fra den ene lastterminalen til den andre:

Med fjerningen av de to batteriene er den totale motstanden målt på dette stedet lik R1 og R3 parallelt: 0,8 Ω. Dette er vår «Thevenin-motstand» (RThevenin) for ekvivalent krets:

Bestem spenningen over lastmotstanden
Med lastmotstanden (2 Ω) festet mellom tilkoblingspunktene, kan vi bestemme spenningen over den og strøm gjennom det som om hele nettverket ikke var noe mer enn en enkel seriekrets:

Legg merke til at spenningen og strømtallene for R2 (8 volt, 4 ampere) er identiske med de som ble funnet ved hjelp av andre analysemetoder. Legg også merke til at spennings- og strømtallene for motstanden fra Thevenin-serien og Thevenin-kilden (totalt) ikke gjelder noen komponent i den originale, komplekse kretsen. Thevenins teorem er bare nyttig for å bestemme hva som skjer med en enkelt motstand i et nettverk: belastningen.
Fordelen er selvfølgelig at du raskt kan bestemme hva som vil skje med den enkelte motstanden hvis den var av en annen verdi enn 2 Ω uten å måtte gjennomgå mye analyse igjen. Bare koble den andre verdien for lastmotstanden til Thevenin-ekvivalente krets, og litt seriekretsberegning vil gi deg resultatet.
ANMELDELSE:
- Thevenins teorem er en måte å redusere et nettverk til en ekvivalent krets sammensatt av en enkelt spenningskilde, seriemotstand og serielast.
- Fremgangsmåte for Thevenins teorem:
- Finn Thevenin-kildespenningen ved å fjerne lastmotstanden fra den opprinnelige kretsen og beregne spenningen over de åpne tilkoblingspunktene der lastmotstanden pleide å være.
- Finn Thevenin-motstanden ved å fjerne alle strømkilder i den originale kretsen (spenningskilder kortsluttet og nåværende kilder åpne) og beregne total motstand mellom de åpne tilkoblingspunktene.
- Tegn Thevenin-ekvivalent krets, med Thevenin-spenningskilden i serie med Thevenin-motstanden. Lastmotstanden festes på nytt mellom de to åpne punktene i den tilsvarende kretsen.
- Analyser spenning og strøm for lastmotstanden etter reglene for seriekretser.
RELATERT ARBEIDSBLAD:
- Thevenins, Nortons og Maximum Power Transfer Theorems Worksheet