A sum er resultatet av et tillegg. For eksempel, å legge til 1, 2, 3 og 4 gir summen 10, skrevet
 |
(1)
|
Tallene som summeres kalles tillegg, eller noen ganger summander. Sammendragsoperasjonen kan også indikeres ved hjelp av en stor signatur med øvre og nedre grenser skrevet over og under, og indeksen angitt nedenfor. For eksempel kan summen ovenfor skrives
 |
(2)
|
The summen av en liste med tall er implementert som Total.
En sum
 |
(3)
|
der hvert begrep 
er gitt av noen faste regler (dvs. 
er en brønn -definert sekvens) kalles en (endelig) serie, og hvis antall ord 
er uendelig, kalles summen en uendelig serie (eller ofte bare en «serie»). En sum av skjemaet
 |
(4)
|
kalles en geometrisk serie .
Vilkår for konvergens av en serie kan bestemmes i Wolfram-språket ved hjelp av SumConvergence.
Den generelle endelige maktsummen
 |
(5)
|
kan gis ved uttrykket
 |
(6)
|
som tilsvarer Faulhabers formel, der notasjonen 
betyr mengden i spørsmålet heves til riktig kraft 
og alle vilkår i skjemaet 
erstattes med det tilsvarende Bernoulli-tall 
.
En morsom identitet på grunn av J. Ziegenbein (pers. comm., 19. juni 2002) følger av identiteten
 |
(7)
|
som kan skrives
 |
(8)
|
Derfor 
, for eksempel, kan skrives i tilsvarende former
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
og så videre.
Nicomachus teorem gir som nysgjerrig uttrykk for maktsummen 
.
Spesielle summer inkluderer
 |
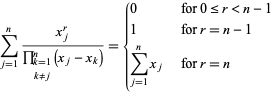(13)
|
og
 |
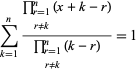(14)
|
For å minimere summen av et sett med firkanter av tall 
om et gitt tall 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
ta derivatet.
 |
(17)
|
Løsning for 
gir
 |
(18)
|
så 
minimeres når 
er satt til mener.