Introduksjon til k-nærmeste naboer: En kraftig maskinlæringsalgoritme (med implementering i Python & R)

Merk: Denne artikkelen ble opprinnelig publisert 10. oktober 2014 og oppdatert 27. mars 2018

Oversikt

• Forstå k nærmeste nabo (KNN) – en av de mest populære maskinlæringsalgoritmene
• Lær hvordan kNN fungerer i python
• Velg riktig verdi av k i enkle termer

Innledning

I løpet av de fire årene av min datavitenskaplige karriere har jeg bygget mer enn 80% klassifiseringsmodeller og bare 15-20% regresjonsmodeller. Disse forholdene kan være mer eller mindre generaliserte i hele bransjen. Årsaken bak denne skjevheten mot klassifiseringsmodeller er at de fleste analytiske problemer innebærer å ta en beslutning.

Vil en kunde for eksempel skrive eller ikke, skal vi målrette kunden X mot digitale kampanjer, enten kunden har et høyt potensial eller ikke osv. Disse analysene er mer innsiktsfulle og direkte knyttet til en implementeringskart.

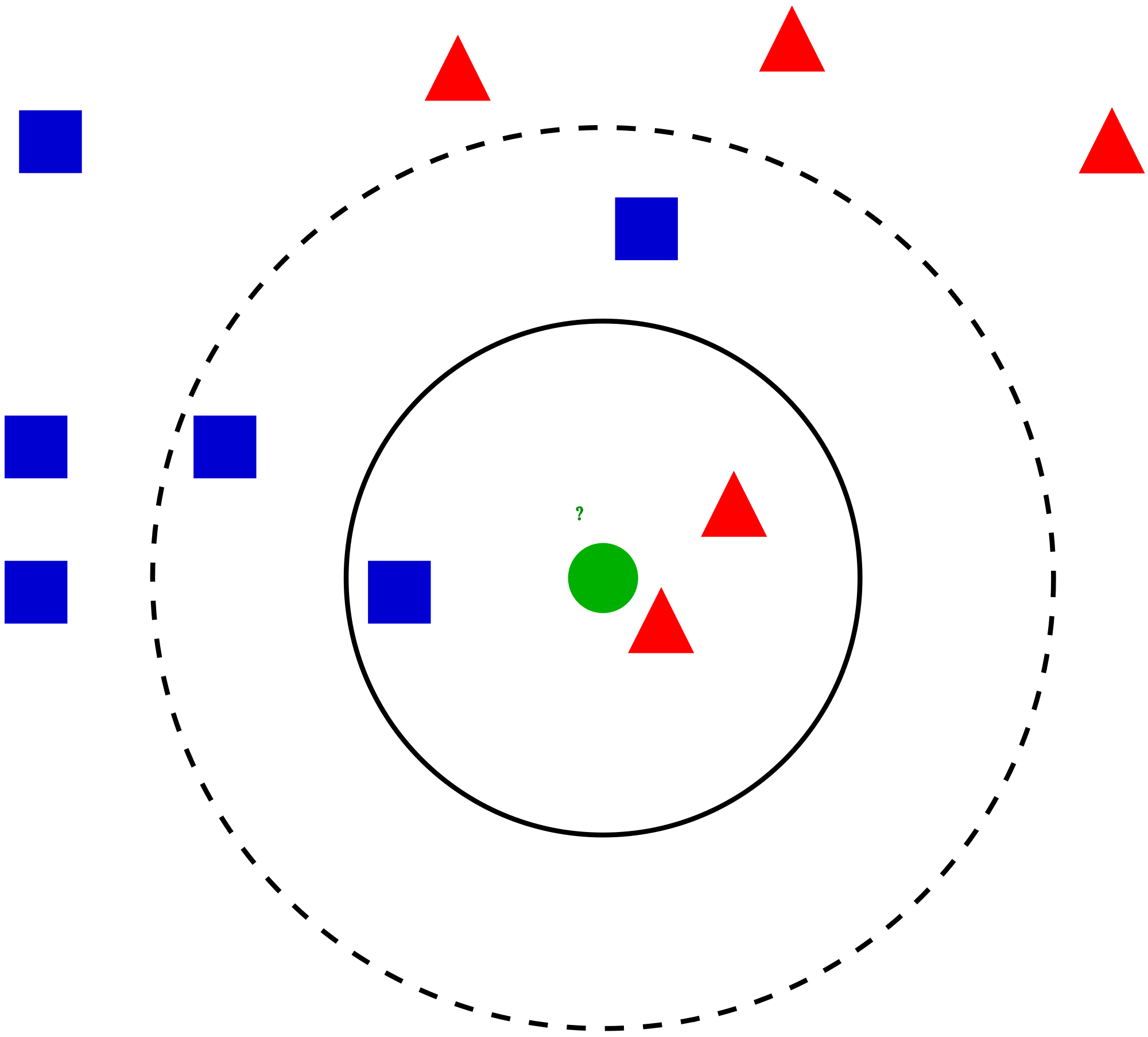
I denne artikkelen vil vi snakke om en annen mye brukt klassifiseringsteknikk for maskinlæring som kalles K-nærmeste naboer (KNN). Vårt fokus vil primært være på hvordan algoritmen fungerer, og hvordan påvirker inngangsparameteren utdata / prediksjon.

Merk: Folk som foretrekker å lære gjennom videoer, kan lære det samme gjennom vårt gratis kurs – K- Nærmeste naboer (KNN) -algoritme i Python og R. Og hvis du er en helt nybegynner for datalogi og maskinlæring, kan du sjekke ut vårt Certified BlackBelt-program –

• Certified AI & ML Blackbelt + -program

Innholdsfortegnelse

• Når bruker vi KNN-algoritme?
• Hvordan fungerer KNN-algoritme fungerer?
• Hvordan velger vi faktoren K?
• Breaking it Down – Pseudo Code of KNN
• Implementering i Python fra bunnen av
• Sammenligning av modellen vår med scikit-learning

Når bruker vi KNN-algoritme?

KNN kan brukes til begge prediktive problemer med klassifisering og regresjon. Det er imidlertid mer brukt i klassifiseringsproblemer i bransjen. For å evaluere en hvilken som helst teknikk ser vi generelt på tre viktige aspekter:

1. Lett å tolke utdata

2. Beregningstid

3. Prediktiv kraft

La oss ta noen eksempler for å plassere KNN i skalaen:

KNN algoritme messer over alle parametere av hensyn. Det brukes ofte for sin enkle tolkning og lave beregningstid.

Hvordan fungerer KNN-algoritmen?

La oss ta en enkel sak for å forstå denne algoritmen. Følgende er en spredning av røde sirkler (RC) og grønne firkanter (GS):

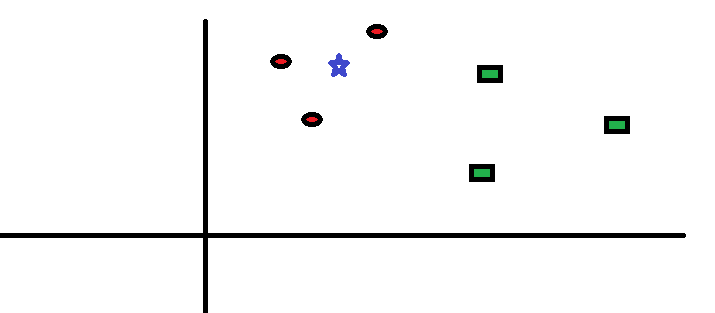Du har tenkt å finne ut klassen til den blå stjernen (BS). BS kan enten være RC eller GS og ingenting annet. «K» er KNN-algoritmen er den nærmeste nabo vi ønsker å ta avstemningen fra. La oss si K = 3. Derfor vil vi nå lage en sirkel med BS som sentrum like stor som å bare legge inn tre datapunkter på flyet . Se følgende diagram for mer informasjon:

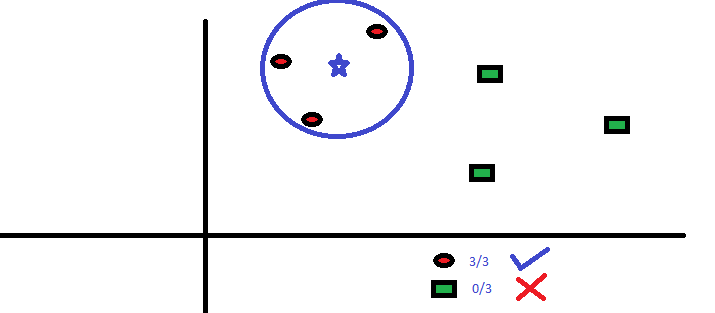De tre nærmeste punktene til BS er alle RC. med et godt konfidensnivå, kan vi si at BS skal tilhøre klassen RC. Her ble valget veldig tydelig da alle tre stemmer fra nærmeste nabo gikk til RC. Valget av parameter K er veldig avgjørende i denne algoritmen Deretter vil vi forstå hva som er faktorene som skal anses for å konkludere med den beste K.

Hvordan velger vi faktoren K?

La oss først prøve å forstå hva K påvirker nøyaktig i algoritmen. Hvis vi ser det siste eksemplet, gitt at alle de 6 treningsobservasjonene forblir konstante, med en gitt K-verdi, kan vi lage grenser for hver klasse. se grenser vil skille RC fra GS. På samme måte, la oss prøve å se effekten av verdien «K» på klassegrensene. Følgende er de forskjellige grensene som skiller de to klassene med forskjellige verdier av K.

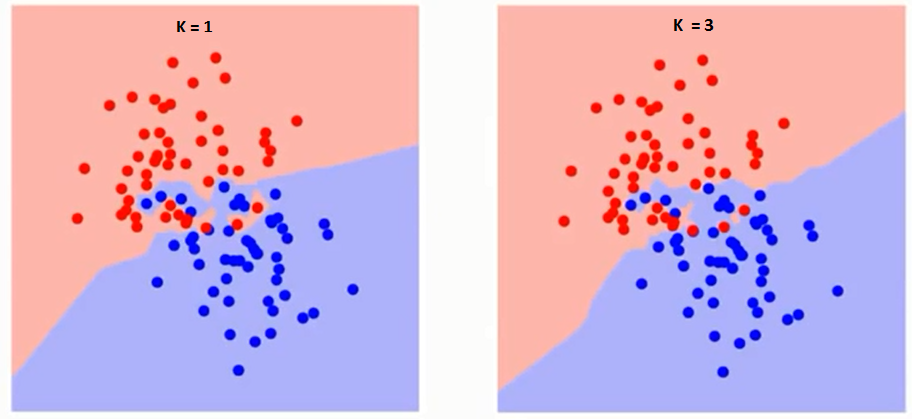
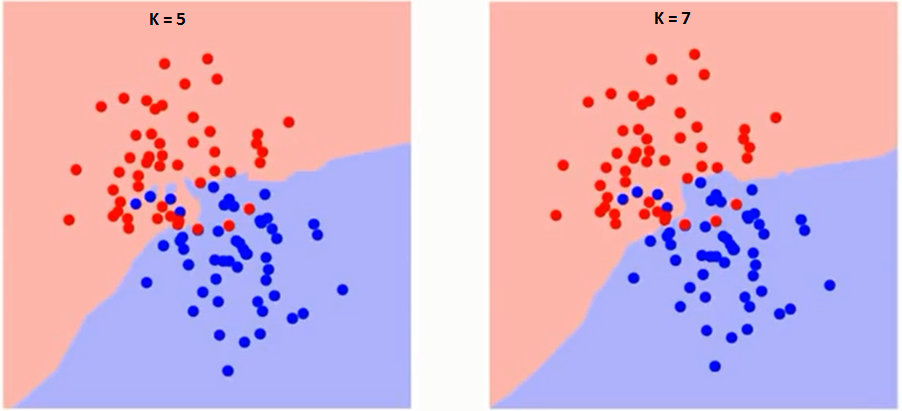
Hvis du følger nøye med, kan du se at grensen blir jevnere med økende verdi av K. Når K øker til uendelig, blir den til slutt blå eller helt rød avhengig av det totale flertallet. Treningsfeilfrekvensen og valideringsfeilfrekvensen er to parametere vi trenger for å få tilgang til forskjellige K-verdier. Følgende er kurven for treningsfeilraten med en varierende verdi på K:

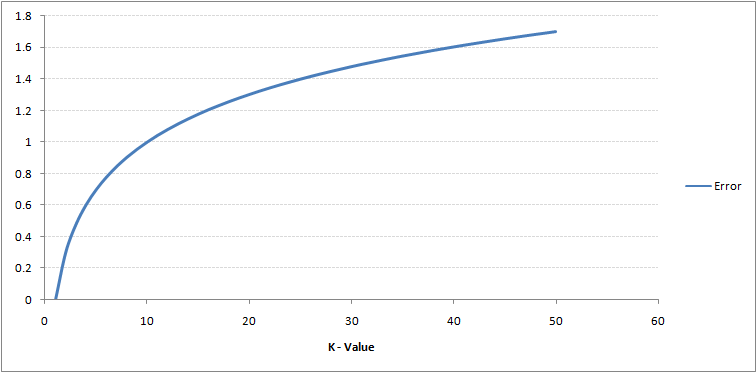Som du kan se, feilrate ved K = 1 er alltid null for treningsutvalget.Dette er fordi det nærmeste punktet for et treningsdatapunkt er selve. Forutsigelsen er derfor alltid nøyaktig med K = 1. Hvis valideringsfeilkurve hadde vært lik, ville vårt valg av K ha vært 1. Følgende er valideringsfeilkurve med varierende verdi på K:

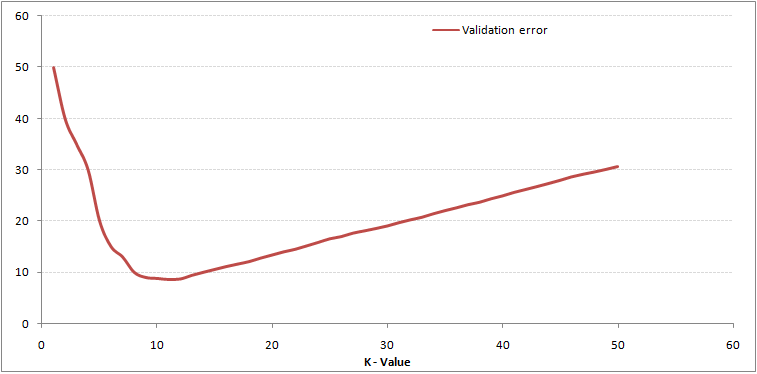Dette gjør historien tydeligere. Ved K = 1 overmonterte vi grensene. Derfor reduseres feilraten til å begynne med og når et minimum. Etter minima-punktet øker det med økende K. For å få den optimale verdien av K, kan du adskille opplæring og validering fra det opprinnelige datasettet. Nå plott valideringsfeilkurven for å få den optimale verdien av K. Denne verdien av K skal brukes for alle spådommer.

Innholdet ovenfor kan forstås mer intuitivt ved hjelp av vårt gratis kurs – K-nærmeste naboer ( KNN) Algoritme i Python og R

Breaking it Down – Pseudo Code of KNN

Vi kan implementere en KNN-modell ved å følge trinnene nedenfor:

1. Last inn dataene
2. Initialiser verdien av k
3. For å få den forutsagte klassen, skal du gå fra 1 til totalt antall treningsdatapunkter
   1. Beregn avstanden mellom testen data og hver rad med treningsdata. Her vil vi bruke euklidisk avstand som avstandsmåling, siden det er den mest populære metoden. De andre beregningene som kan brukes er Chebyshev, cosinus osv.
   2. Sorter de beregnede avstandene i stigende rekkefølge basert på avstandsverdier
   3. Få topp k-rader fra den sorterte matrisen
   4. Få den hyppigste klassen av disse radene
   5. Returner den forutsagte klassen

Implementering i Python fra bunnen av

Vi bruker det populære Iris-datasettet for å bygge vår KNN-modell. Du kan laste den ned herfra.

Sammenligning av modellen vår med scikit-learning

Vi kan se at begge modellene forutsa samme klasse (Iris- virginica ) og de samme nærmeste naboene (). Derfor kan vi konkludere med at modellen vår kjører som forventet.

Implementering av kNN i R

Trinn 1: Importere dataene

Trinn 2: Kontrollere dataene og beregne datasammendraget

Output

Trinn 3: Deling av data

Trinn 4: Beregning den euklidiske avstanden

Trinn 5: Skrive funksjonen for å forutsi kNN

Trinn 6: Beregning av etiketten (Navn) for K = 1

Output

For K=1 "Iris-virginica"

På samme måte kan du beregne for andre verdier av K.

Sammenligning av kNN-prediktorfunksjonen vår med «Class» -biblioteket

Output

For K=1 "Iris-virginica"

Vi kan se at begge modeller spådde samme klasse (Iris-virginica).

Sluttnotater

KNN-algoritme er en av de enkleste klassifiseringsalgoritmene. Selv med slik enkelhet, kan det gi svært konkurransedyktige resultater. KNN-algoritme kan også brukes til regresjonsproblemer. Den eneste forskjellen fra den omtalte metoden vil man bruke gjennomsnitt av nærmeste naboer i stedet for å stemme fra nærmeste naboer. KNN kan kodes i en enkelt linje på R. Jeg skal ennå utforske hvordan vi kan bruke KNN-algoritme på SAS.

Fant du artikkelen nyttig? Har du brukt noe annet maskinlæringsverktøy nylig? Planlegger du å bruke KNN i noen av dine forretningsproblemer? Hvis ja, del med oss hvordan du planlegger å gjøre det.

Hvis du liker det du nettopp har lest &, vil du fortsette din analytiske læring, abonner på e-post, følg oss på twitter eller liker facebooksiden vår.