Slope
I tillegg til den kjente betydningen har ordet «skråning» presis matematisk betydning. Skråningen til en linje er stigningen over løpeturen, eller endringen i y delt på endringen i x. For å finne skråningen på en linje, velg to punkter på linjen. Deretter trekker du x-koordinatene og trekker y-koordinatene i samme rekkefølge. Del forskjellen på y-koordinatene med forskjellen på x- koordinatene:
Gitt to punkter (x1, y1) og (x2, y2) på en linje er skråningen på linjen lik:
m = =
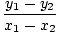
Negativ stigning
Hvis en linje har en positiv skråning (dvs. m > 0), da øker alltid y når x øker og y alltid reduseres når x reduseres. Dermed begynner linjediagrammet nederst til venstre og går mot øvre høyre.
Ofte er imidlertid skråningen på en linje negativ. En negativ skråning innebærer at y alltid avtar når x øker og y alltid øker når x avtar. Her er et eksempel på en graf med negativ stigning:
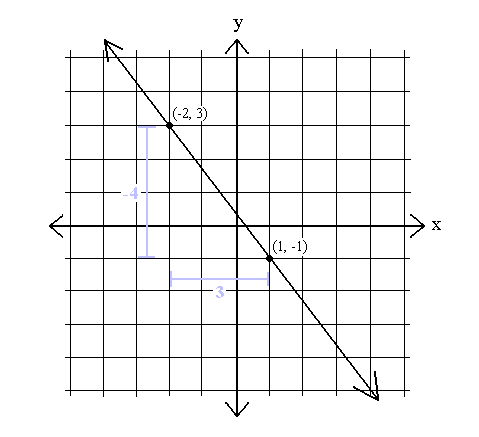
m =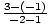 
= 
= – 
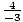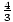
Når x øker med 3, reduseres y med 4, og når x reduseres med 3, øker y med 4.
Horisontale og vertikale linjer
Noen ganger , vil vi se ligninger hvis grafer er horisontale linjer. Dette er grafer der y forblir konstant – det vil si y1 – y2 = 0 for to punkter på linjen:
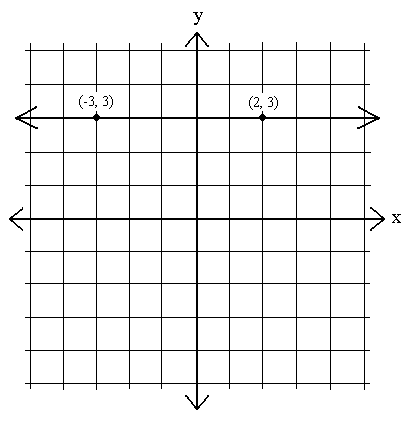
m =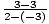 
= 
= 0.
Helningen på en horisontal linje er 0. Med andre ord, når x øker eller avtar, endres ikke y. x tar alle mulige verdier til en spesifikk y-verdi.
Vi vil også se ligninger hvis grafer er vertikale linjer. Dette er grafer der x forblir konstant – det vil si x1 – x2 = 0 for to punkter på linjen:
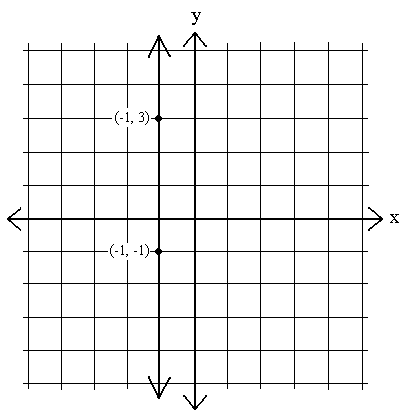
m =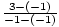 
= 
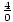= udefinert. Vi kan ikke dele et tall med null.
Skråningen til en loddrett linje er udefinert.x øker eller reduseres ikke; heller tar y alle mulige verdier til en bestemt x-verdi.