Hva er BFS algoritme (Breadth-First Search)?
Breadth-first search (BFS) er en algoritme som brukes til å tegne data eller søke i tre eller kryssende strukturer. Den fulle formen for BFS er det første søket etter bredde.
Algoritmen besøker og merker effektivt alle nøkkelknutepunktene i en graf på en nøyaktig bredde. Denne algoritmen velger en enkelt node (innledende eller kildepunkt) i en graf og besøker deretter alle nodene ved siden av den valgte noden. Husk at BFS får tilgang til disse nodene en etter en.
Når algoritmen besøker og markerer startnoden, beveger den seg mot nærmeste ubesøkte noder og analyserer dem. Når de er besøkt, blir alle noder merket. Disse gjentakelsene fortsetter til alle nodene i grafen har blitt besøkt og merket.
I denne opplæringen om algoritme vil du lære:
- Hva er BFS-algoritme (bredde-første søk)?
- Hva er grafgjennomganger?
- Arkitekturen til BFS-algoritme
- Hvorfor trenger vi BFS-algoritme?
- Hvordan fungerer BFS-algoritme?
- Eksempel på BFS-algoritme
- Regler for BFS-algoritme
- Anvendelser av BFS-algoritme
Hva er grafgjennomganger?
En grafgjennomgang er en vanlig metode for å lokalisere toppunktposisjonen i grafen. Det er en avansert søkealgoritme som kan analysere grafen med hastighet og presisjon sammen med å markere sekvensen til de besøkte toppunktene. Denne prosessen lar deg raskt besøke hver node i en graf uten å bli låst i en uendelig løkke.
Arkitekturen til BFS-algoritme
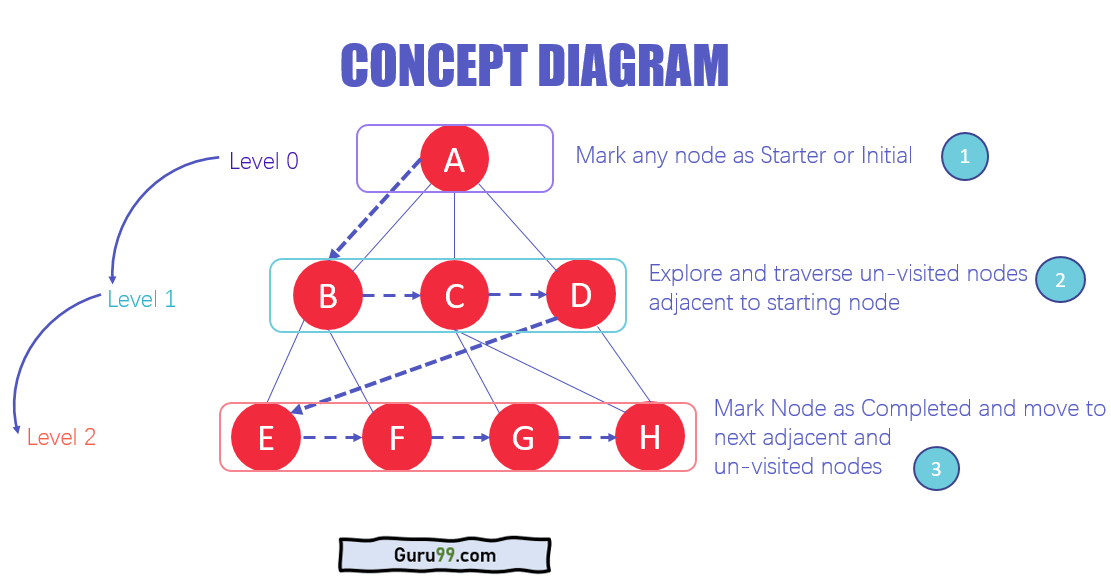
- I de forskjellige nivåene i dataene kan du merke hvilken som helst node som start eller startnode for å begynne å krysse. BFS vil besøke noden og merke den som besøkt og plasserer den i køen.
- Nå vil BFS besøke de nærmeste og ubesøkte noder og markere dem. Disse verdiene blir også lagt til i køen. Køen fungerer på FIFO-modellen.
- På lignende måte analyseres de gjenværende nærmeste og ubesøkte nodene i grafen merket og legges til i køen. Disse elementene slettes fra køen når de mottas og skrives ut som resultat.
Hvorfor trenger vi BFS-algoritme?
Det er mange grunner til å bruke BFS-algoritmen som skal brukes til å søke etter datasettet ditt. Noen av de viktigste aspektene som gjør denne algoritmen til ditt førstevalg er:
- BFS er nyttig for å analysere nodene i en graf og konstruere den korteste veien for å krysse gjennom disse.
- BFS kan krysse gjennom en graf i det minste antall iterasjoner.
- Arkitekturen til BFS-algoritmen er enkel og robust.
- Resultatet av BFS-algoritmen har et høyt nøyaktighetsnivå sammenlignet med andre algoritmer.
- BFS-iterasjoner er sømløse, og det er ingen mulighet for at denne algoritmen blir fanget i et uendelig løkkeproblem.
Hvordan fungerer BFS-algoritme?
Grafgjennomgang krever at algoritmen besøker, sjekker og / eller oppdaterer hver eneste ubesøkte node i en trelignende struktur. Grafoverganger er kategorisert etter rekkefølgen de besøker nodene i grafen.
BFS-algoritme starter operasjonen fra den første eller startnoden i en graf og krysser den grundig. Når den vellykket krysser den opprinnelige noden, blir neste ikke-kryssede toppunkt i grafen besøkt og merket.
Derfor kan du si at alle nodene ved siden av dagens toppunkt blir besøkt og krysset i den første iterasjonen. En enkel kømetodikk brukes til å implementere arbeidet med en BFS-algoritme, og den består av følgende trinn:
Trinn 1)

Hvert toppunkt eller node i grafen er kjent. For eksempel kan du merke noden som V.
Trinn 2)

Hvis toppunktet V ikke er tilgjengelig, legg deretter til toppunktet V i BFS-køen
Trinn 3)

Start BFS-søket, og merk ferdig toppunkt V som besøkt etter fullføring.
Trinn 4)

BFS-køen er fortsatt ikke tom, fjern derfor toppunktet V for grafen fra køen.
Trinn 5)

Hent alle gjenværende hjørner på grafen som ligger ved siden av toppunktet V
Trinn 6)

For hvert tilstøtende toppunkt, la oss si V1, hvis det ikke er besøkt ennå, legg deretter til V1 i BFS-køen
Trinn 7)

BFS besøker V1 og merker det som besøkt og sletter det fra køen.
Eksempel BFS-algoritme
Trinn 1)

Du har en graf over syv tall fra 0 – 6.
Trinn 2)

0 eller null er merket som en rotnode.
Trinn 3)

0 besøkes, merkes og settes inn i kødatastrukturen.
Trinn 4)
Gjenværende 0 tilstøtende og ubesøkte noder blir besøkt, merket og satt inn i køen.
Trinn 5)

Gjennomgang av gjentakelser gjentas til alle noder blir besøkt.
Regler for BFS-algoritme
Her er viktige regler for bruk av BFS-algoritme:
- En kø (FIFO-først inn først ut) datastruktur brukes av BFS.
- Du markerer hvilken som helst node i grafen som rot og begynner å krysse dataene fra den.
- BFS krysser alle nodene i grafen og slipper dem som fullførte.
- BFS besøker en tilstøtende ubesøkt node, merker den som ferdig og setter den inn i en kø.
- Fjerner forrige toppunkt fra køen i tilfelle ingen tilstøtende toppunkt blir funnet.
- BFS-algoritme gjentas til alle hjørnene i grafen er vellykket krysset og merket som fullført.
- Det er ingen sløyfer forårsaket av BFS under gjennomkjøring av data fra en hvilken som helst node.
Bruk av BFS-algoritme
La oss ta en se på noen av de virkelige applikasjonene der en BFS-algoritmeimplementering kan være svært effektiv.
- Uveide grafer: BFS-algoritme kan enkelt lage den korteste banen og et minimum spennende tre for å besøke alle hjørnene i grafen på kortest mulig tid med høy nøyaktighet.
- P2P-nettverk: BFS kan implementeres for å finne alle nærmeste eller nærliggende noder i et peer-to-peer-nettverk. Dette vil finne de nødvendige dataene raskere .
- Web-crawlere: Søkemotorer eller web-crawlere kan enkelt bygge flere nivåer av indekser ved å bruke BFS. BFS-implementering starter fra kilden, som er websiden, og deretter besøker den alle koblingene fra den kilden .
- Navigasjonssystemer: BFS kan hjelpe deg med å finne alle de nærliggende stedene fra hoved- eller kildeplassering.
- Network Broadcast ing: En kringkastet pakke styres av BFS-algoritmen for å finne og nå alle nodene den har adressen til.
Sammendrag
- En grafgjennomgang er en unik prosess som krever at algoritmen besøker, sjekker og / eller oppdaterer hver eneste ubesøkte node i en trelignende struktur. BFS algoritme fungerer på et lignende prinsipp.
- Algoritmen er nyttig for å analysere nodene i en graf og konstruere den korteste banen for å krysse gjennom disse.
- Algoritmen krysser grafen i det minste antall iterasjoner og på kortest mulig tid.
- BFS velger en enkelt node (innledende eller kildepunkt) i en graf og besøker deretter alle nodene ved siden av den valgte noden. BFS får tilgang til disse nodene en etter en.
- De besøkte og merkede dataene plasseres i kø av BFS. En kø fungerer på en første inn-ut-basis. Derfor blir elementet som er plassert i grafen først slettet først og skrevet ut som et resultat.
- BFS-algoritmen kan aldri bli fanget i en uendelig sløyfe.
- På grunn av høy presisjon og robust implementering brukes BFS i flere virkelige løsninger som P2P-nettverk, webcrawlere, og Network Broadcasting.