Hvordan varierer trykket med volumendring under adiabatisk ekspansjon og kompresjon i en ideell gass? Denne siden er et vedlegg til vår diskusjon om lyd. Luft ved atmosfæretrykk er en nesten ideell gass, og lydoverføring i luft er nær adiabatisk for normale frekvenser og overføringsavstander. (Vi kommer tilbake til denne antagelsen nedenfor.)
Den første loven om termodynamikk relaterer endringen i intern energi dU til arbeidet dW utført av et system og varmen dQ lagt til den.
dU = dQ – dW
Per definisjon, i en adiabatisk prosess, vekslet varmen dQ = 0. Å erstatte dette i første lov og omorganisere gir
0 = dQ = dU + dW
Det andre begrepet er enkelt: arbeidet utført dW når et system endrer volumet V med dV er PdV.
Den første termen kan være relatert til den spesifikke varmen, som er definert som tilført varme per enhet endring av temperatur per mol stoff. Hvis vi tilfører varme med konstant volum, ekspanderer ikke gassen, og det fungerer ikke. Så den tilførte varmen øker den indre energien U. Så det følger at definisjonen at den spesifikke varmen ved konstant volum er ![]() , hvor n er antall mol. Derfor
, hvor n er antall mol. Derfor
Nå er tilstandsligningen til en ideell gass
nRT = PV ( ii)
der R er gasskonstanten. Tar derivater gir
Vi kan nå kombinere ligninger (i) og (iii) for å eliminere T. (i) og (ii) gi henholdsvis disse uttrykkene for ncv dT:
Å samle PdV- og VdP-vilkårene gir
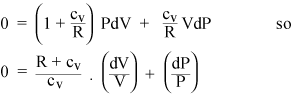
Hvis gassen nå er ideell, er dens indre energi all kinetisk, så den interne energien U avhenger bare av T. Fra tilstandsligningen til en ideell gass (ii) kan vi beregne arbeidet dW utført ved konstant trykk: det er bare PdV = nRdT. Så hvis vi tilfører en gass varme ved konstant trykk, må vi ekstra varme RdT for hvert mol gass, utover varmen vi burde legge til med konstant volum. Så den spesifikke varmen til en ideell gass ved konstant trykk er bare cP = cv + R. Forholdet mellom spesifikke varmer er gitt et standardsymbol:
. Så vi har
(iv)
Dette er hovedresultatet som vi trenger for å diskutere lydbølger: vi har nettopp vist at proporsjonal trykkendring er – γ ganger proporsjonal volumendring eller γ ganger proporsjonal endring i tetthet.
La oss ikke stoppe her, for vi er bare noen få linjer unna et viktig resultat. Vi vet at d (ln x) = dx / x (se kalkulator for et bevis). Så vi kan skrive den forrige ligningen som
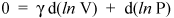
og omorganisere den for å gi
(v)
Derfor for en adiabatisk prosess i en ideell gass,
. (vi)
Ved refleksjon er du enig i at cP > cV: At konstant volum, alle th varmen du legger i går til å øke den indre energien og dermed øke temperaturen. Ved konstant trykk må du ikke bare legge inn varmen som øker den indre energien, men også en mengde varme som tilsvarer arbeidet som gjøres når systemet gjennomgår termisk utvidelse. For luft er γ omtrent 1,4.
Selvfølgelig kan vi nå erstatte i (vi) fra tilstandsligningen (ii) for å se hvordan P og T eller T og V er relatert til en adiabatisk prosess.
Når er lyd adiabatisk?
Vi nevnte ovenfor at «lydoverføring i luft er nær adiabatisk for normale frekvenser og overføringsavstander». Når mislykkes dette? Ved trykkmaxima i en lydbølge er temperaturen høy. Så vi forventer at noe varme vil diffundere til de nærliggende trykkminima. Selvfølgelig, i en halv periode med en lydbølge, er det ikke mye tid for varme å diffundere en halv bølgelengde. Tiden det tar for varmen å diffundere går imidlertid som kvadratet på avstanden. Så denne prosessen er mindre ubetydelig for høye frekvenser, fordi den kortere halvbølgelengden mer enn kompenserer for den kortere halvperioden. Denne diffusjonen tar mekanisk energi ut av bølgen, spesielt ved høye frekvenser, og effekten øker med overføringsavstand.Av denne grunn (og noen ganger andre) er fjerne lyder ikke bare mindre høye, men også mindre lyse enn nære.