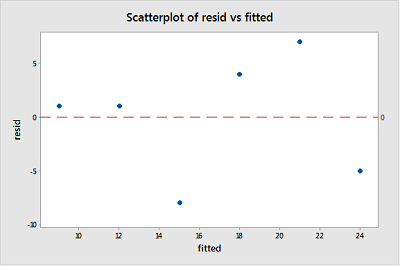
Når du utfører en restanalyse, er et «residuals versus fit plot» det hyppigst opprettede plottet. Det er et spredningsdiagram av rester på y-aksen og tilpassede verdier (estimerte responser) på x-aksen. Plottet brukes til å oppdage ikke-linearitet, ulik feilavvik og outliers.
La oss se på et eksempel for å se hvordan et «veloppdragen» restplott ser ut. Noen forskere (Urbano- Marquez, et al., 1989) var interessert i å bestemme om alkoholforbruk var lineært relatert til muskelstyrke. Forskerne målte det totale levetidsforbruket av alkohol (x) på et tilfeldig utvalg av n = 50 alkoholholdige menn. De målte også styrken (y) av deltamuskelen i hver persons ikke-dominerende arm. Et tilpasset linjediagram over de resulterende dataene, (alcoholarm.txt), ser ut som:
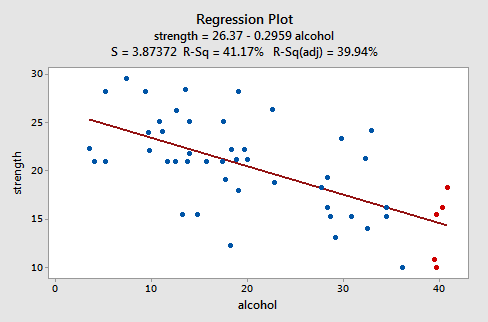
Handlingen antyder at det er et avtagende lineært forhold mellom alkohol og armstyrke. Det antyder også at det ikke er uvanlige datapunkter i datasettet. Og det illustrerer at variasjonen rundt den estimerte regresjonslinjen er konstant, noe som antyder at antagelsen om like feilvariasjoner er rimelig.
Her ser de korresponderende restene versus passer-plottet ut for datasettet. enkel lineær regresjonsmodell med armstyrke som respons og alkoholforbruk som prediktor:
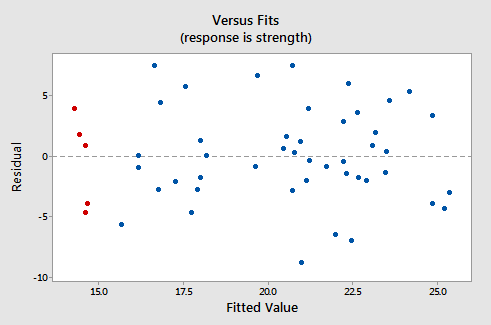
Merk at, som definert, restene vises på y-aksen og de tilpassede verdiene vises på x-aksen. Du bør være i stand til å se tilbake på spredningsdiagrammet for dataene og se hvordan datapunktene der tilsvarer datapunktene i rest versus versus-plot her. Hvis du har problemer med å gjøre det, kan du se på de fem datapunktene i det opprinnelige spredningsdiagrammet som vises i rødt. Merk at den forventede responsen (tilpasset verdi) til disse mennene (hvis alkoholforbruk er rundt 40) er omtrent 14 Legg også merke til mønsteret der de fem datapunktene avviker fra den estimerte regresjonslinjen.
Se nå på hvordan og hvor disse fem datapunktene vises i residual versus versus plot. Deres tilpassede verdi er ca 14 og deres avvik fra residual = 0 linjen har samme mønster som avviket fra den estimerte regresjonslinjen. Ser du sammenhengen? Ethvert datapunkt som faller direkte på den estimerte regresjonslinjen har en rest på 0. Derfor er rest = 0-linjen tilsvarer den estimerte regresjonslinjen.
Dette plottet er et klassisk eksempel på en veloppdragen rest vs. passt-plot. Her er kjennetegnene til en veloppdragen rest vs. passer-plot og hva de foreslå om hensiktsmessigheten til det enkle e lineær regresjonsmodell:
- Restene «spretter tilfeldig» rundt 0-linjen. Dette antyder at antagelsen om at forholdet er lineær er rimelig.
- Restene danner omtrent et «horisontalt bånd» rundt 0-linjen. Dette antyder at avvikene i feiluttrykkene er like.
- Ingen rest «skiller seg ut» fra det grunnleggende tilfeldige mønsteret for residualer. Dette antyder at det ikke er noen outliers.
Generelt sett vil du at gjenværende vs. passer-tomter skal se ut som plottet ovenfor. Ikke glem at tolkning av disse plottene er subjektiv. Min erfaring har vært at studenter som lærer restanalyse for første gang, har en tendens til å fortolke disse plottene, og ser på hver vri og vri som noe potensielt plagsomt. Du vil spesielt ønsker å vær forsiktig med å legge for mye vekt på gjenværende vs. passer-tomter basert på små datasett. Noen ganger er datasettene bare for små til at det er verdt å tolke en rest vs. Ikke bekymre deg! Du lærer – med øvelse – hvordan du «leser» disse plottene.