Anta at luft pumpes nedover et glatt rundt rør, som har en konstant diameter bortsett fra et snitt i midten der røret smalner ned til halve diameteren, og utvides deretter igjen. Anta at alle endringene i diameter skjer jevnt, og luften strømmer jevnt nedover røret uten hvirvler eller turbulens.
Trening
hvor i røret forventer du trykket for å være størst?
Svar
De fleste spurte dette for første gang forutsi at trykket vil være størst i den smale delen av røret. Men faktisk, hvis vi faktisk gjør eksperimentet, ved å sette trykkmålere på forskjellige punkter langs røret, finner vi, mot intuitivt, at lufttrykket er lavest der luften beveger seg raskest!

For å se hvordan dette kan være, vil vi bruke teknikkene vi utviklet for å finne ut hvordan trykket varierte i en stasjonær væske. Måten vi gjorde det på, var å tegne et fritt kroppsdiagram for en liten sylinder med væske. Siden denne lille sylinderen var i ro, var den totale kraften på den null, så nettotrykket balanserte vekten. Vurder nå en jevn flytende væske. Det er nyttig å visualisere strømmen ved å tegne strømlinjer, linjer slik at retningen deres er retningen væsken beveger seg i på hvert punkt.

Egentlig forteller disse strømlinjeformene deg ikke bare retningen væsken beveger seg i, men gir også en ide om hastigheten – der de kommer nærmere hverandre, må væsken bevege seg raskere, fordi samme mengde væske strømmer gjennom en smalere region. Tenk deg nå en sylinder med luft som beveger seg langs røret, dens akse parallelt med strømlinjen. Åpenbart må den øke hastigheten når den kommer inn i den smale delen av røret – siden samme mengde luft strømmer gjennom den smale delen som den brede delen, må den gå raskere.
Men hvis den lille væskesylinder akselererer, må den påvirkes av en kraft som skyver den bakfra.
Vekten er ikke relevant her, siden den beveger seg horisontalt. Derfor er den eneste kraften som virker på det, trykket, og vi må konkludere med at trykket på baksiden er større enn trykket på fronten. Derfor må trykket synke når det kommer inn i den smale delen. For å gjøre det tydeligere hva som skjer, tegner vi en ganske stor sylinder:
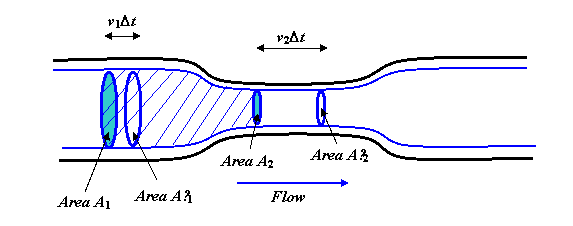
Væsken flyter jevnt og jevnt langs røret. De tykke blå linjene er strømlinjeformede. Du kan faktisk forestille deg å rotere hele diagrammet rundt sentralaksen for å få et tredimensjonalt bilde, og de blå linjene vil bli en sylinder, med en smalere «nakkesnitt», som ekko formen til rør.
Tenk nå på væskelegemet i strømlinjene som er vist, og avgrenset i de to endene av de sirkulære områdene A1 og A2. Strømningshastigheten for væske over A1 må være den samme som hastigheten på flyte over A2, fordi i jevn flyt ikke væske kan hoppes opp i midten (eller tømmes derfra heller). Volumet som strømmer over A1 på ett sekund er v1A1. (For å se dette, forestill deg et langt rett rør uten et smalt del. Hvis væsken strømmer med, si 3 meter per sekund, så vil alt væske som var innenfor 3 meter fra området A1 på oppstrømsiden i løpet av ett sekund ha strømmet gjennom.)
Så, flyt over A1 er lik flyt over A2, \
(Fotnote: Det er kanskje verdt å nevne at vi implisitt antar veloci ty er den samme på alle punkter i område A1. Enhver ekte væske har noe viskositet (friksjon) og vil bevege seg langsommere nær sidene av røret enn i midten. Vi vil diskutere dette senere. Foreløpig anser vi en «ideal» væske, begrepet som brukes når man ignorerer viskositet. Faktisk er resultatet vi får ok – vi kunne ha tatt et lite område A1 langt unna sidene, slik at hastigheten ville ha vært det samme for hele området, men det ville gitt et mye mindre tydelig diagram.)
Vi er nå klare til å undersøke økningen i væskeens kinetiske energi når den øker i den smale delen, og forstå hvordan trykkforskjellen utførte arbeidet som var nødvendig for å øke hastigheten.
\
Den eneste mulige kilden for denne økningen i energi er arbeidet som gjøres ved å presse væsken inn i den smale delen.
\
Så dette er arbeidet som gjøres på vår væskebit ved at væsken skyver den bakfra – men det er ikke slutten på historien, fordi vår del av væske i seg selv virker med å skyve væsken foran seg, så for å finne den totale økningen i klumpens energi, må vi trekke fra det eksterne arbeidet det gjør.Det vil si at det totale arbeidet som er utført av presset på væsken vår er
\
å huske at \ (A_1v_1 = A_2v_2 \).
Dette arbeidet må utgjøre endringen i kinetisk energi, så
\
hvorfra
\
Dette er Bernoullis ligning.
\.
Bidragsytere og attribusjoner
- Michael Fowler (Beams Professor, Department of Physics, University of Virginia)