튜브가 좁아지는 중간 부분을 제외하고 일정한 직경을 가진 부드러운 원형 튜브로 공기가 펌핑된다고 가정합니다. 직경의 절반으로 줄인 다음 다시 넓어집니다. 직경의 모든 변화가 원활하게 일어나고 공기가 소용돌이 나 난기류없이 꾸준히 튜브 아래로 흐른다 고 가정합니다.
운동
튜브 어디에서 기대하십니까? 가장 큰 압력이 될까요?
답변
대부분의 사람들은 처음으로이 질문에 대해 압력이 튜브의 좁은 부분에서 가장 클 것이라고 예측합니다. 그러나 실제로 튜브를 따라 여러 지점에 압력 게이지를 배치하여 실험을 실제로 수행하면 공기가 가장 빠르게 움직이는 곳에서 공기압이 가장 낮다는 것을 직관적으로 알 수 있습니다!

이게 어떻게 될 수 있는지 알아보기 위해 고정 유체에서 압력이 어떻게 변하는 지 알아보기 위해 개발 한 기술입니다. 우리가 그렇게 한 방법은 작은 액체 실린더에 대한 자유 신체 다이어그램을 그리는 것이 었습니다. 이 작은 실린더는 정지되어 있었기 때문에 총 힘은 0이었고, 순 압력이 무게의 균형을 맞췄습니다. 이제 꾸준히 움직이는 유체를 고려하십시오. 흐름을 시각화하여 흐름을 시각화하는 데 도움이됩니다. 흐름의 방향이 각 지점에서 유체가 이동하는 방향이되도록 유선으로 선을 그립니다.

실제로 이러한 유선은 유체가 이동하는 방향을 알려줄뿐만 아니라 속도에 대한 아이디어도 제공합니다. 서로 가까워지는 곳에서는 동일한 양의 유체가 흐르기 때문에 유체가 더 빨리 이동해야합니다. 좁은 지역을 통해. 이제 유선과 평행 한 축을 따라 파이프를 따라 움직이는 공기 실린더를 상상해보십시오. 당연히 튜브의 좁은 부분으로 들어가면서 속도가 빨라져야합니다. 좁은 부분은 넓은 부분과 같은 양의 공기가 흐르기 때문에 더 빨리 진행되어야합니다.
유체 실린더가 가속되고있는 경우 뒤쪽에서 밀어내는 힘에 의해 작용해야합니다.
여기서 무게는 수평으로 움직이기 때문에 관련이 없습니다. 따라서 그것에 작용하는 유일한 힘은 압력이며, 우리는 뒤쪽의 압력이 앞쪽의 압력보다 크다는 결론을 내려야합니다. 따라서 좁은 부분에 들어가면 압력이 떨어져야합니다. 무슨 일이 일어나고 있는지 더 명확하게하기 위해 다소 큰 원통을 그립니다.
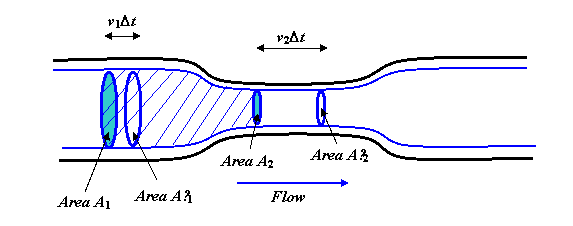
유체가 꾸준히 부드럽게 흐르고 있습니다. 파이프. 굵은 파란색 선은 유선입니다. 사실 3 차원 그림을 얻기 위해 전체 다이어그램을 중심 축을 중심으로 회전하는 것을 상상해야합니다. 파란색 선은 더 좁은 “목”섹션이있는 원통이되어 모양을 반영합니다. 파이프.
이제 표시된 유선 내에서 두 끝이 원형 영역 A1과 A2로 막혀있는 유체의 몸체를 고려합니다. A1을 통과하는 유체의 흐름 속도는 다음의 속도와 같아야합니다. 일정한 흐름에서는 유체가 중간에 쌓일 수 없기 때문에 (또는 거기에서 고갈 될 수 없기 때문에) A2를 가로 지르는 흐름입니다. 1 초 동안 A1을 가로 지르는 부피는 v1A1입니다. (이것을 보려면 좁은 파이프가없는 긴 직선 파이프를 상상해보십시오. 유체가 초당 3 미터로 흐르면 1 초 안에 상류 측 A1 영역의 3 미터 이내에 있던 모든 유체가 통과하게됩니다.)
그래서, A1을 가로 지르는 흐름은 A2를 가로 지르는 흐름과 동일합니다. \
(각주 : veloci를 암시 적으로 가정하고 있다는 것을 언급 할 가치가 있습니다. ty는 A1 영역의 모든 지점에서 동일합니다. 실제 유체는 약간의 점성 (마찰)이 있으며 중간보다 파이프 측면 근처에서 더 느리게 이동합니다. 나중에 논의 할 것입니다. 지금은 점도를 무시할 때 사용되는 용어 인 “이상적인”유체를 고려합니다. 사실 우리가 도출 한 결과는 괜찮습니다. 측면에서 멀리 떨어진 작은 영역 A1을 가져 와서 속도가 전체 영역에 대해 동일하지만 훨씬 덜 명확한 다이어그램을 제공했을 것입니다.)
이제 유체가 좁은 부분으로 속도를 낼 때 유체의 운동 에너지 증가를 조사 할 준비가되었습니다. 압력 차가 속도를 높이는 데 필요한 작업을 어떻게했는지 이해합니다.
\
이 에너지 증가의 유일한 원인은 유체를 압력으로 밀어 넣는 작업입니다. 좁은 부분입니다.
\
그래서 이것은 유체 덩어리를 뒤에서 밀어내는 유체에 의해 수행되는 작업입니다. 그러나 이것이 이야기의 끝이 아닙니다. 유체 자체가 유체를 앞쪽으로 밀어내는 역할을하므로 덩어리 에너지의 총 증가를 찾으려면 외부 작업에서 빼야합니다.즉, 유체에 대한 압력으로 수행되는 총 작업은
\
\ (A_1v_1 = A_2v_2 \)를 기억하는 것입니다.
이 작업은 동일해야합니다. 운동 에너지의 변화, 그래서
\
그로부터
\
이것은 Bernoulli의 방정식입니다.
\.
기여자 및 기여
- Michael Fowler (버지니아 대학교 물리학과 빔스 교수)