이상 기체에서 단열 팽창 및 압축 중에 압력이 부피 변화에 따라 어떻게 변합니까? 이 페이지는 소리에 대한 논의에 대한 부록입니다. 대기압의 공기는 거의 이상적인 기체이며 공기 중의 사운드 전송은 정상 주파수 및 전송 거리에서 단열에 가깝습니다. (아래의 가정으로 돌아갑니다.)
열역학의 첫 번째 법칙은 내부 에너지 dU의 변화를 시스템이 수행 한 작업 dW 및 여기에 추가 된 열 dQ와 관련시킵니다.
dU = dQ – dW
정의에 따라 단열 과정에서 교환 된 열 dQ = 0. 첫 번째 법칙에서 이것을 대체하고 재정렬하면
0 = dQ = dU + dW
두 번째 용어는 쉽습니다. 시스템이 볼륨 V를 dV로 변경할 때 dW로 수행되는 작업은 PdV입니다.
첫 번째 용어는 물질 몰당 단위 온도 변화 당 추가되는 열로 정의되는 비열과 관련 될 수 있습니다. 일정한 부피의 열을 추가하면 가스가 팽창하지 않아 작동하지 않습니다. 따라서 추가 된 열은 내부 에너지 U를 증가시킵니다. 따라서 일정한 부피의 비열이 , 여기서 n은 몰의 수입니다. 따라서
이제 이상 기체 상태 방정식은
nRT = PV ( ii)
여기서 R은 기체 상수입니다. 미분을하면
이제 방정식 (i)와 (iii)을 결합하여 T를 제거 할 수 있습니다. (i) (ii) ncv dT에 대해 각각 다음 식을 제공합니다.
PdV 및 VdP 용어를 수집하면
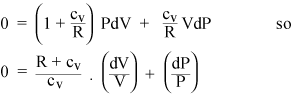
이제 기체가 이상적인 경우 내부 에너지는 모두 운동이므로 내부 에너지 U는 T에만 의존합니다. 이상 기체의 상태 방정식 (ii)에서 다음을 계산할 수 있습니다. 일정한 압력에서 수행 된 작업 dW : 단지 PdV = nRdT입니다. 따라서 일정한 압력에서 가스에 열을 추가하면 가스의 각 몰에 대해 RdT를 추가로 가열해야합니다. 열을 일정 부피로 추가해야합니다. 따라서 일정한 압력에서 이상 기체의 비열은 cP = cv + R입니다. 비열의 비율에는 표준 기호가 지정됩니다.
. 그래서 우리는
(iv)
이것이 음파를 논의하기 위해 필요한 주요 결과입니다. 압력의 비례 변화가 – 부피의 비례 변화의 γ 배 또는 밀도의 비례 변화의 γ 배라는 것을 방금 보여주었습니다.
하지만 여기서 멈추지 말자. 중요한 결과에서 몇 줄 떨어져 있기 때문입니다. d (ln x) = dx / x라는 것을 알고 있습니다 (미적분학 참조). 따라서 다음과 같이 쓸 수 있습니다.
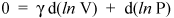
정렬하여 제공
(v)
따라서 이상 기체의 단열 과정
. (vi)
반성하면 cP > cV : 일정한 볼륨, 모든 일 당신이 넣은 열은 내부 에너지를 증가시켜 온도를 상승시킵니다. 일정한 압력에서 내부 에너지를 높이는 열뿐만 아니라 시스템이 열팽창을 겪을 때 수행되는 작업과 동일한 열량을 넣어야합니다. 공기의 경우 γ는 약 1.4입니다.
물론, 우리는 이제 상태 방정식 (ii)에서 (vi)로 대체하여 P와 T 또는 T와 V가 단열 과정과 어떻게 관련되어 있는지 확인할 수 있습니다.
음은 언제 단열됩니까?
위에서 “공중에서의 소리 전달은 정상 주파수와 전송 거리에서 단열에 가깝습니다”라고 언급했습니다. 언제 실패합니까? 음파의 최대 압력에서는 온도가 높습니다. 따라서 일부 열이 인접 압력 최소값으로 확산 될 것으로 예상합니다. 물론 음파의 반주기에는 열이 반 파장을 확산시킬 시간이 많지 않습니다. 그러나 열이 확산되는 데 걸리는 시간은 거리의 제곱으로 이동합니다. 따라서이 과정은 고주파에 대해 무시할 수없는 정도입니다. 짧은 반파 장이 짧은 반주기를 보상하는 것보다 더 많기 때문입니다. 이 확산은 특히 고주파수에서 파동에서 기계적 에너지를 빼앗아 전송 거리에 따라 그 효과가 증가합니다.이러한 이유로 (그리고 때로는 다른) 멀리있는 소리는 가까운 소리보다 덜 클뿐만 아니라 덜 밝습니다.