Thevenin ’s Theorem은 부하에 연결된 단일 전압 소스와 직렬 저항 만있는 등가 회로로 아무리 복잡하더라도 모든 선형 회로를 단순화 할 수 있다고 말합니다. “선형”의 자격은 중첩 정리에서 발견 된 것과 동일합니다. 여기서 모든 기본 방정식은 선형이어야합니다 (지수 또는 근이 없어야 함). 수동 구성 요소 (예 : 저항 및 나중에 인덕터 및 커패시터)를 다루는 경우 ), 이것은 사실입니다. 그러나 비선형적인 일부 구성 요소 (특히 특정 가스 방전 및 반도체 구성 요소)가 있습니다. 즉, 전압 및 / 또는 전류에 따른 전류 변화에 대한 반대입니다. 따라서 이러한 구성 요소를 포함하는 회로를 호출합니다. 구성 요소 유형, 비선형 회로.
전력 시스템의 테 브닌 정리
테 브닌 정리는 특히 회로에서 특정 저항 ( “부하”라고 함)이있는 전력 시스템 및 기타 회로를 분석하는 데 유용합니다. ”저항)은 변경 될 수 있으며, 부하 저항의 각 시험 값과 함께 회로를 다시 계산하여 부하 저항을 통과하는 전압과 전류를 결정해야합니다. 예제 회로를 다시 살펴 보겠습니다.

R2를 “부하”저항으로 지정하기로 결정했다고 가정 해 보겠습니다. R2의 전압과 R2를 통한 전류를 결정하는 데 사용할 수있는 4 가지 분석 방법 (분기 전류, 메시 전류, Millman의 정리 및 중첩 정리)이 이미 있지만 이러한 각 방법은 시간이 많이 걸립니다. 부하 저항이 변경 될 경우 어떤 일이 발생하는지 찾기 위해 이러한 방법 중 하나를 반복해서 반복한다고 상상해보십시오 (여러 부하가 필요에 따라 켜지고 꺼지기 때문에 부하 저항을 변경하는 것은 전력 시스템에서 매우 일반적입니다. 병렬 연결의 총 저항이 변경됨) 한 번에 연결되는 수에 따라 다름). 이것은 잠재적으로 많은 작업이 필요할 수 있습니다!
Thevenin 등가 회로
Thevenin의 정리는 일시적으로 부하 저항을 제거하여이를 쉽게 만듭니다. 원래 회로와 동등한 cir로 남은 것을 줄입니다. 단일 전압 소스와 직렬 저항으로 구성된 큐. 부하 저항은이 “Thevenin 등가 회로”에 다시 연결될 수 있으며 전체 네트워크가 단순한 직렬 회로 인 것처럼 계산이 수행됩니다.

… Thevenin 변환 후…
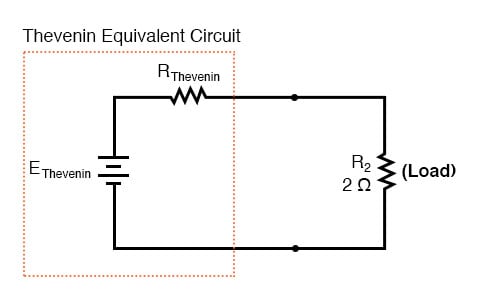
“Thevenin 등가 회로” 부하 저항 (R2)이 연결되는 두 지점에서 볼 수있는 B1, R1, R3 및 B2의 전기적 등가입니다.
올바르게 유도 된 경우 Thevenin 등가 회로는 다음과 정확히 동일하게 동작합니다. B1, R1, R3 및 B2에 의해 형성된 원래 회로. 즉, 부하 저항 (R2) 전압과 전류는 두 회로에서 동일한 부하 저항 값에 대해 정확히 동일해야합니다. 부하 저항 R2는 EThevenin 및 RThevenin의 값이 올바르게 계산 된 경우 B1, R1, R3 및 B2의 원래 네트워크와 EThevenin 및 RThevenin의 Thevenin 등가 회로 간의 “차이점”을 말할 수 없습니다.
물론 더 간단한 회로로 “Thevenin 변환”을 수행 할 때의 장점은 원래 네트워크에서보다 부하 전압과 부하 전류를 훨씬 쉽게 해결할 수 있다는 것입니다. 등가 Thevenin 소스 전압과 직렬 저항을 계산하는 것은 실제로 매우 쉽습니다. 먼저 선택한 부하 저항이 원래 회로에서 제거되고 브레이크 (개방 회로)로 대체됩니다.

Thevenin 결정 전압
다음으로 부하 저항을 연결하는 데 사용 된 두 지점 사이의 전압이 결정됩니다. 이를 위해 원하는 분석 방법을 사용하십시오. 이 경우 부하 저항이 제거 된 원래 회로는 반대 배터리가있는 단순한 직렬 회로에 지나지 않으므로 직렬 회로의 규칙, 옴의 법칙 및 Kirchhoff의 전압을 적용하여 개방 부하 단자의 전압을 결정할 수 있습니다. 법칙 :

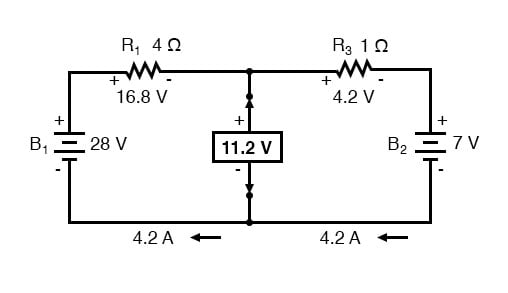
두 개의 부하 연결 지점은 배터리 전압 중 하나와 저항기 전압 강하 중 하나에서 11.2V로 나옵니다.이것은 등가 회로의 “Thevenin 전압”(EThevenin)입니다.

Thevenin 직렬 저항 결정
등가 회로에 대한 Thevenin 직렬 저항을 찾으려면 원래 회로 (부하 저항이 제거 된 상태)를 가져 와서 전원을 제거해야합니다 (중첩 정리에서했던 것과 동일한 스타일 : 전압 소스가 단선으로 교체 된 전선 및 전류 소스) 한 부하 단자에서 다른 부하 단자로의 저항을 계산합니다.

제거시 두 배터리 중이 위치에서 측정 된 총 저항은 R1 및 R3 병렬로 0.8Ω입니다. 이것은 등가 회로에 대한 “Thevenin 저항”(RThevenin)입니다.

부하 저항의 전압 결정
연결 지점 사이에 연결된 부하 저항 (2Ω)을 사용하여 전압을 결정할 수 있습니다. 및 전류 전체 네트워크가 단순한 직렬 회로에 불과한 것처럼 보입니다.

R2의 전압 및 전류 수치에 유의하십시오. (8 볼트, 4 암페어)는 다른 분석 방법을 사용하여 찾은 것과 동일합니다. 또한 Thevenin 직렬 저항 및 Thevenin 소스 (전체)에 대한 전압 및 전류 수치는 원래의 복잡한 회로의 구성 요소에 적용되지 않습니다. Thevenin의 정리는 네트워크의 단일 저항 (부하)에 어떤 일이 발생하는지 결정하는 데만 유용합니다.
물론 장점은 단일 저항에 어떤 일이 발생하는지 신속하게 결정할 수 있다는 것입니다. 다시 많은 분석을 거치지 않고 2Ω 이외의 값. 부하 저항의 다른 값을 Thevenin 등가 회로에 연결하면 약간의 직렬 회로 계산이 결과를 얻을 수 있습니다.
리뷰 :
- Thevenin의 정리 네트워크를 단일 전압 소스, 직렬 저항 및 직렬 부하로 구성된 등가 회로로 줄이는 방법입니다.
- Thevenin의 정리를 위해 따라야 할 단계 :
- Thevenin 소스 전압 찾기 원래 회로에서 부하 저항을 제거하고 부하 저항이 있던 개방 된 연결 지점의 전압을 계산합니다.
- 원래 회로의 모든 전원을 제거하여 Thevenin 저항을 찾습니다 (전압 소스가 단락 됨). 개방 된 연결 지점 사이의 총 저항을 계산합니다.
- Thevenin 전압 소스를 Thevenin 저항과 직렬로 연결하여 Thevenin 등가 회로를 그립니다. 부하 저항은 등가 회로의 두 개방 지점 사이에 다시 연결됩니다.
- 직렬 회로 규칙에 따라 부하 저항의 전압과 전류를 분석합니다.
관련 워크 시트 :
- Thevenin s, Norton s 및 Maximum Power Transfer Theorems 워크 시트