압력과 부피의 관계 : 보일의 법칙
가스에 가해지는 압력이 증가하면 가스 입자가 서로 밀착되기 때문에 가스의 부피가 감소합니다. 반대로 가스의 압력이 감소하면 가스 부피가 증가합니다. 기체 입자는 이제 더 멀리 이동할 수 있습니다. 기체의 부피가 증가하기 때문에 기상 풍선이 대기를 통해 더 낮은 압력의 영역으로 상승함에 따라 더 커집니다. 즉, 대기 기체가 풍선 표면에 더 적은 압력을가하므로 내부 가스는 내부 및 외부 압력이 같을 때까지 팽창합니다.
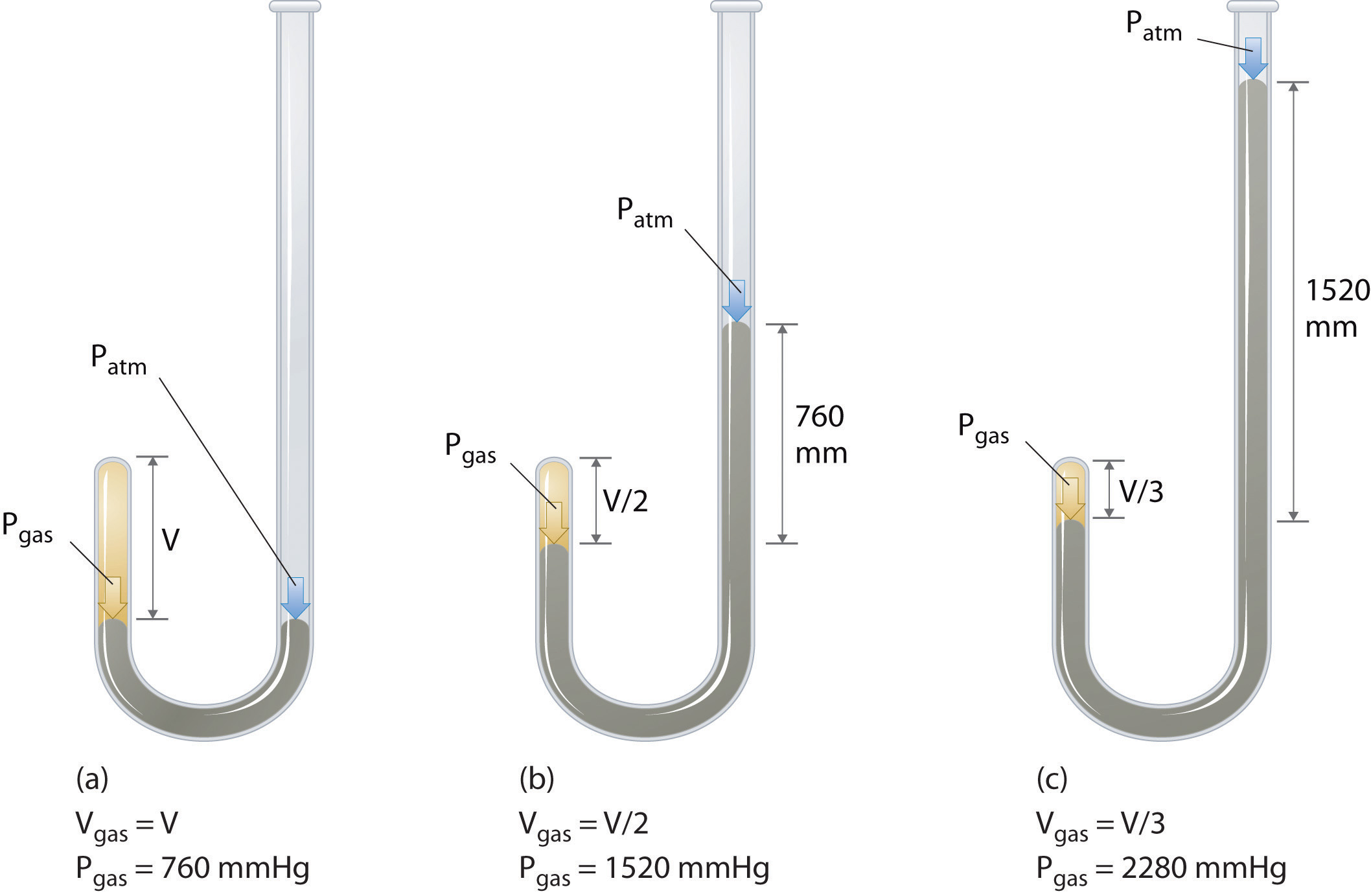
아일랜드의 화학자 Robert Boyle (1627–1691)은 압력과 부피 사이의 양적 관계를 결정하는 초기 실험을 수행했습니다. 가스. 보일은 그림 \ (\ PageIndex {1} \)와 같이 부분적으로 수은으로 채워진 J 자형 튜브를 사용했습니다. 이 실험에서는 소량의 가스 나 공기가 수은 기둥 위에 갇혀 있고 그 부피는 대기압과 일정한 온도에서 측정됩니다. 그런 다음 가스 샘플에 대한 압력을 높이기 위해 더 많은 수은이 열린 암에 부어집니다. 가스에 가해지는 압력은 대기압에 수은 기둥 높이의 차이를 더한 값이며 그 결과 부피가 측정됩니다. 이 과정은 열린 암에 더 이상 공간이 없거나 가스의 부피가 너무 작아 정확하게 측정 할 수 없을 때까지 반복됩니다. Boyle의 자체 실험 중 하나와 같은 데이터는 여러 가지 방식으로 표시 될 수 있습니다 (그림 \ (\ PageIndex {2} \)). \ (V \) 대 \ (P \)의 간단한 플롯은 쌍곡선이라는 곡선을 제공하고 압력과 체적 사이의 역 관계를 보여줍니다. 압력이 두 배가되면 체적이 2 배 감소합니다. 두 수량 간의 관계는 다음과 같이 설명됩니다.
\
양변을 \ (P \)로 나누면 \ (P \)와 \ 사이의 역 관계를 나타내는 방정식이 제공됩니다. (V \) :
\
또는
\
여기서 ∝ 기호는 “에 비례합니다.” 따라서 V 대 1 / P의 플롯은 기울기가 Equations \ (\ ref {10.3.1} \) 및 \ (\ ref {10.3.3} \)의 상수와 동일한 직선입니다. P 대신 V에 의한 방정식 \ (\ ref {10.3.1} \)은 P와 1 / V 사이에 유사한 관계를 제공합니다. 상수의 수치는 실험에 사용 된 가스의 양과 온도에 따라 달라집니다. 이 압력과 부피의 관계는 발견 자 이후 보일의 법칙으로 알려져 있으며 다음과 같이 표현할 수 있습니다. 일정한 온도에서 일정량의 가스의 부피는 압력에 반비례합니다. 실제 법률은 그림 \ (\ PageIndex {2} \)에 나와 있습니다.
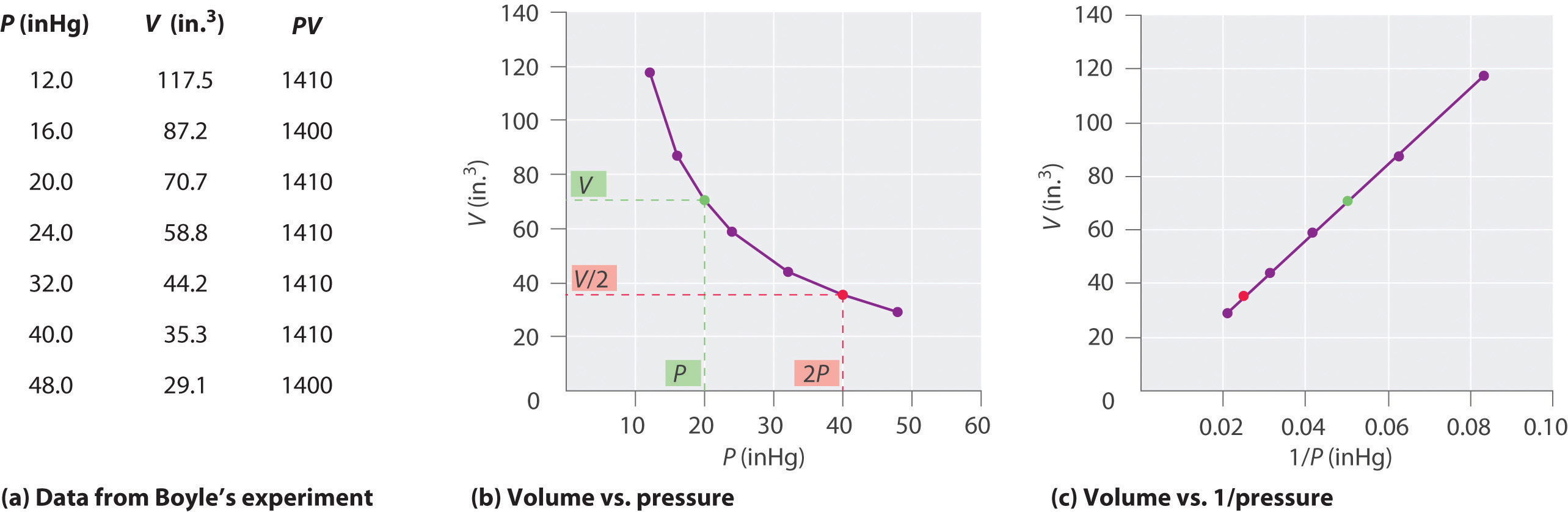
일정한 온도에서 일정량의 가스 부피는 압력에 반비례합니다.