대수 > 합계 >
MathWorld 기여자 > Ziegenbein >
![]()
A 합계는 더하기의 결과입니다. 예를 들어 1, 2, 3, 4를 더하면 합계 10이됩니다.
| |
(1)
|
합산되는 숫자를 가산 또는 때로는 합산이라고합니다. 합산 연산은 상한과 하한이 위와 아래에 쓰여진 대문자 시그마와 아래에 표시된 인덱스를 사용하여 표시 될 수도 있습니다. 예를 들어 위의 합계를 작성할 수 있습니다.
| |
(2)
|
숫자 목록의 합계는 합계로 구현됩니다.
합계
| |
(3)
|
각 용어 ![]() 는 고정 된 규칙에 의해 주어집니다 (예 :
는 고정 된 규칙에 의해 주어집니다 (예 : ![]() 는 우물입니다. -정의 된 시퀀스)를 (유한) 시리즈라고하며,
는 우물입니다. -정의 된 시퀀스)를 (유한) 시리즈라고하며, ![]() 항의 수가 무한이면 합계를 무한 시리즈 (또는 종종 “시리즈”)라고합니다. 양식의 합계
항의 수가 무한이면 합계를 무한 시리즈 (또는 종종 “시리즈”)라고합니다. 양식의 합계
| |
(4)
|
는 기하학적 시리즈라고합니다. .
SumConvergence를 사용하여 Wolfram 언어에서 계열 수렴 조건을 결정할 수 있습니다.
일반 유한 전력 합계
| |
(5)
|
표현식으로 제공 가능
| |
(6)
|
Foulhaber의 공식과 동일합니다. 여기서 표기법 ![]() 는 질문은 적절한 거듭 제곱
는 질문은 적절한 거듭 제곱 ![]() 로 제기되고
로 제기되고 ![]() 형식의 모든 용어가 해당하는 Bernoulli 번호
형식의 모든 용어가 해당하는 Bernoulli 번호 ![]() .
.
J. Ziegenbein (pers. comm., June 19, 2002)는 신원을 따름
| |
(7)
|
작성 가능
| |
(8)
|
그러므로 ![]() 는 동등한 형식으로 작성할 수 있습니다.
는 동등한 형식으로 작성할 수 있습니다.
| |
|
|
(9)
|
| |
|
|
(10)
|
| |
|
|
(11)
|
| |
|
|
(12)
|
등.
Nicomachus의 정리는 거듭 제곱 합계 ![]() 에 대한 흥미로운 표현을 제공합니다.
에 대한 흥미로운 표현을 제공합니다.
특별 합계에는 다음이 포함됩니다.
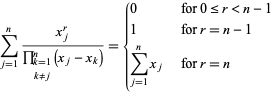 |
(13)
|
및
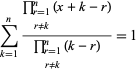 |
(14)
|
정사각형 집합의 합을 최소화하려면 주어진 숫자에 대한 숫자 ![]()
![]()
| |
|
|
(15 )
|
| |
|
|
(16)
|
미분을 가져옵니다.
| |
(17)
|
![]() 를 풀면
를 풀면
| |
(18)
|
![]() 는
는 ![]() 가 의미합니다.
가 의미합니다.