 |
円は簡単に作成できます: 中心点から など: すべてのポイントは中心から同じ距離にあります。 |

自分で描くことができます
ボードにピンを入れ、その周りにひものループを入れて、挿入しますループに鉛筆。文字列を伸ばしたまま円を描きます!
Play With It
ポイントをドラッグして、半径と円周がどのように変化するかを確認してください。
(維持できるかどうかを確認してください一定の半径!)
半径、直径、円周

半径は中心から外側への距離です。
直径は円を真っ直ぐ横切って中心を通ります。
円周は距離です。
そしてこれが本当にクールなことです:
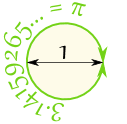
円周を直径で割ると、3.141592654 …
これは数値π(Pi)
|
したがって、直径が1の場合、円周は3.141592654 … |
 |
私たちは言うことができます:
円周=π×直径
例:直径100mの円を歩きますが、どこまで歩きましたか?
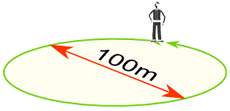
歩行距離=周囲径=π×100m
= 314m(最も近いmまで)
直径は半径の2倍であることに注意してください:
直径= 2×半径
したがって、これも当てはまります:
円周= 2× π×半径
要約:
| ×2 | ×π |
| |
|
| 半径 | 直径 | 周囲 |
覚えている
単語の長さは覚えやすいかもしれません:
- 半径最短の単語で短い推定値
- 直径が長い
- 円周が最も長い
定義
 |
円は平面(2次元)なので、次のようになります。 |
円:中心から一定の距離にある平面上のすべての点のセット。
面積

円の面積は、半径の2乗のπ倍です。記述:
A =πr2
ここで
- Aは面積
- rは半径
「円周率は正方形」だと覚えておくために(円周率は通常丸いですが):

例:半径1.2 mの円の面積はどれくらいですか?
または、Diameterを使用します:

A =(π/ 4)×D2
正方形と比較した面積

円の面積は同じ幅の正方形の約80%です。
実際の値は(π/ 4)= 0.785398です。 。= 78.5398 …%
そしてあなたにとって興味深いもの:
線で円の面積を見る
名前
人々が持っているから何千年もの間研究された円には特別な名前が付けられました。
「円の片側から始まり、中心を通り、反対側で終わる線」は、できる限り誰も言いたくありません。 「直径」と言います。
最も一般的な特別な名前は次のとおりです。
線

円が通過するときに円に「触れる」線をタンジェントと呼びます。
円を2点で切断する線を呼びます。 Secant。
円の円周上のある点から別の点に移動する線セグメントは、コードと呼ばれます。
通過する場合中心を通って直径と呼ばれます。
円周の一部は円弧と呼ばれます。

スライス
円には2つの主要な「スライス」があります。
「ピザ」スライスはセクターと呼ばれます。
コードによって作成されたスライスはセグメントと呼ばれます。
一般的なセクター
象限と半円は、2つの特別なタイプのセクターです。

円の四分の一は象限と呼ばれます。

半円は半円と呼ばれます。
内側と外側

円には内側があります そして外側(もちろん!)。 ただし、円の真上にいる可能性があるため、「オン」もあります。
例:「A」は円の外側、「B」は円の内側、「C」は円上にあります。 。

楕円
円は、楕円の「特殊なケース」です。