Mi a BFS algoritmus (Szélesség-első keresés)?
A Szélesség-első keresés (BFS) olyan algoritmus, amelyet adatok ábrázolására, fák vagy bejáró struktúrák keresésére használnak. A BFS teljes formája a Szélesség első keresése.
Az algoritmus hatékonyan meglátogatja és pontosan meghatározza a grafikon összes kulcscsomópontját. Ez az algoritmus egyetlen csomópontot (kezdeti vagy forráspontot) választ ki a grafikonból, majd meglátogatja a kiválasztott csomópont mellett található összes csomópontot. Ne feledje, hogy a BFS egyesével éri el ezeket a csomópontokat.
Miután az algoritmus meglátogatta és megjelöli a kezdő csomópontot, az a legközelebbi meg nem látogatott csomópontok felé halad és elemzi őket. Miután meglátogatta, az összes csomópont meg van jelölve. Ezek az iterációk addig folytatódnak, amíg a grafikon összes csomópontját sikeresen meg nem látogatták és meg nem jelölte.
Ebben az algoritmus oktatóanyagban megtudhatja:
- Mi az a BFS algoritmus (szélesség-első keresés)?
- Mi az a grafikon bejárása?
- A BFS algoritmus architektúrája
- Miért van szükségünk BFS algoritmusra?
- Hogyan működik a BFS algoritmus?
- Példa BFS algoritmusra
- A BFS algoritmus szabályai
- A BFS algoritmus alkalmazásai
Mi a grafikon bejárása?
A gráf bejárása általánosan használt módszer a csúcs pozíciójának a grafikonon történő meghatározására. Ez egy fejlett keresési algoritmus, amely gyorsan és pontosan elemezheti a gráfot, a megjelölt csúcsok sorrendjének megjelölésével együtt. Ez a folyamat lehetővé teszi a grafikon minden csomópontjának gyors meglátogatását anélkül, hogy bezáródna egy végtelen ciklusba.
A BFS algoritmus architektúrája
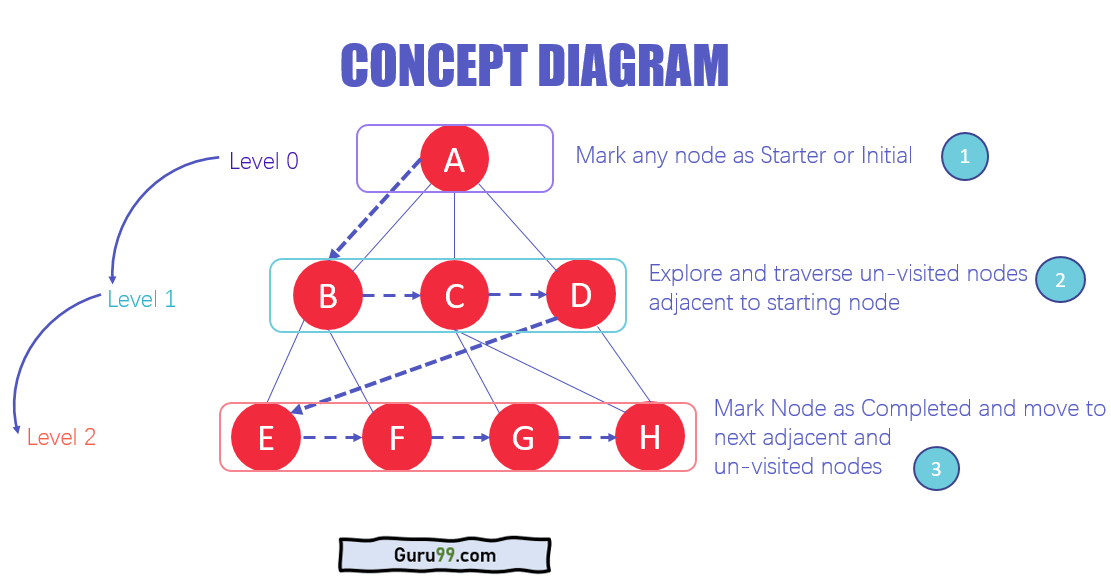
- Az adatok különböző szintjein bármelyik csomópontot kiindulópontként jelölheti meg vagy kezdeti csomópont a bejárás megkezdéséhez. A BFS meglátogatja a csomópontot, meglátogatja látogatottként és elhelyezi a sorban.
- Most a BFS meglátogatja a legközelebbi és fel nem látogatott csomópontokat, és megjelöli őket. Ezek az értékek hozzáadódnak a sorhoz is. A sor a FIFO modellen működik.
- Hasonló módon elemezzük a grafikonon lévő többi legközelebbi és meg nem látogatott csomópontot megjelölve és hozzáadva a sorhoz. Ezeket az elemeket vételként törli a sorból, és ennek eredményeként kinyomtatja őket.
Miért van szükségünk BFS algoritmusra?
Számos oka van annak, hogy a BFS algoritmust felhasználják az adatkészlet keresésére. Néhány legfontosabb szempont, amely ezt az algoritmust választja az első választásnak:
- A BFS hasznos a csomópontok elemzéséhez egy grafikonban és az ezeken való áthaladás legrövidebb útjának felépítéséhez.
- A BFS egy grafikonon keresztül haladhat a legkisebb számú iterációban.
- A BFS algoritmus architektúrája egyszerű és robusztus.
- A BFS algoritmus eredménye nagy pontossággal rendelkezik más algoritmusokhoz képest.
- A BFS iterációk zökkenőmentesek, és nincs esély arra, hogy ez az algoritmus beleakadjon egy végtelen hurok problémába.
Hogyan működik a BFS algoritmus?
A grafikon bejárásához az algoritmusnak meg kell látogatnia, ellenőriznie és / vagy frissítenie kell egy fa-szerű szerkezet minden egyes meg nem látogatott csomópontját. A grafikonok bejárása sorrendbe van sorolva, amelyben meglátogatják a grafikon csomópontjait.
A BFS algoritmus a grafikon első vagy kezdő csomópontjától kezdi a műveletet, és alaposan bejárja azt. Miután sikeresen áthaladt a kezdeti csomóponton, akkor meglátogatja és megjelöli a grafikon következő nem bejárt csúcsát.
Ennélfogva elmondhatja, hogy az aktuális csúccsal szomszédos összes csomópont az első iterációban meglátogatott és bejáratott. Egy egyszerű várakozási módszert alkalmaznak a BFS algoritmus működésének megvalósításához, amely a következő lépésekből áll:
1. lépés)

A grafikon minden csúcsa vagy csomópontja ismert. Például jelölheti a csomópontot V-ként.
2. lépés)

Abban az esetben, ha az V csúcs nem érhető el, vegye fel az V csúcsot a BFS sorba.
3. lépés)

Indítsa el a BFS keresést, és a befejezés után jelölje meg az V. csúcsot meglátogatottként.
4. lépés)

A BFS sor még mindig nem üres, ezért távolítsa el a grafikon V csúcsát a sorból.
5. lépés)

Az összes többi csúcs lekérése a V csúccsal szomszédos grafikonon
6. lépés)

Minden szomszédos csúcsra mondjuk a V1-et, ha még nem látogatta meg, akkor adja hozzá a V1-et a BFS-sorba.
7. lépés)

A BFS meglátogatja a V1-et, megjelöli látogatottként és törli a sorból.
Példa BFS-algoritmusra
1. lépés)

Önnek grafikonja van hét szám 0 és 6 között.
2. lépés)

0 vagy nulla van megjelölve gyökércsomópontként.
3. lépés)

0 meglátogatásra kerül, megjelölik és beszúrják a sor adatstruktúrájába.
4. lépés)
A fennmaradó 0 szomszédos és nem látogatott csomópontot meglátogatja, megjelöli és beszúrja a sorba.
5. lépés)

Az áthaladó iterációkat addig ismételjük, amíg az összes csomópontot meg nem látogatjuk.
A BFS algoritmus szabályai
Itt a BFS algoritmus használatának fontos szabályai vannak:
- Sor (FIFO-First in First Out) adatstruktúra a BFS használja.
- A grafikonon lévő bármelyik csomópontot gyökérként megjelöli, és elkezdi belőle bejárni az adatokat.
- A BFS bejárja a grafikon összes csomópontját, és folyamatosan befejezettként dobja el őket.
- A BFS meglátogat egy szomszédos nem látogatott csomópontot, készként megjelöli és beilleszti egy sorba.
- Eltávolítja az előző csúcsot a sorból, ha nem található szomszédos csúcs.
- A BFS algoritmus addig ismétlődik, amíg a grafikon összes csúcsát sikeresen bejárják és befejezettként jelölik.
- Nincsenek hurkok, amelyeket a BFS okozott egyetlen csomópont adatainak áthaladása során.
A BFS algoritmus alkalmazásai
Vegyünk egy nézzen meg néhány olyan valós alkalmazást, ahol a BFS algoritmus megvalósítása nagyon hatékony lehet.
- Súlyozatlan grafikonok: A BFS algoritmus könnyen létrehozhatja a legrövidebb utat és egy minimális átfedő fát, hogy az összes látogatható legyen. a grafikon csúcsait a lehető legrövidebb időn belül, nagy pontossággal.
- P2P hálózatok: A BFS megvalósítható az összes legközelebbi vagy szomszédos csomópont felkutatásához peer to peer hálózatban. Ez gyorsabban megtalálja a szükséges adatokat .
- Webrobotok: A keresőmotorok vagy a webrobotok könnyen létrehozhatnak többszintű indexeket a BFS alkalmazásával. A BFS megvalósítása a forrásból indul ki, amely a weboldal, majd meglátogatja az adott forrás összes hivatkozását .
- Navigációs rendszerek: A BFS segít megtalálni az összes szomszédos helyet a fő vagy a forrás helyéről.
- Network Broadcast ing: A sugárzott csomagot a BFS algoritmus vezérli, hogy megtalálja és elérje az összes csomópontot, amelynek a címe van.
Összefoglaló
- A grafikon bejárása olyan egyedi folyamat, amelynek megköveteléséhez az algoritmusnak meg kell látogatnia, ellenőriznie és / vagy frissítenie kell minden egyes meg nem látogatott csomópontot egy fa-szerű szerkezet. A BFS algoritmus hasonló elven működik.
- Az algoritmus hasznos a csomópontok elemzéséhez egy grafikonon és az ezeken való áthaladás legrövidebb útjának felépítéséhez.
- Az algoritmus a legkisebb számú ismétléssel és a lehető legrövidebb idő alatt járja be a grafikont.
- A BFS egyetlen csomópontot (kezdeti vagy forráspontot) választ ki a grafikonból, majd meglátogatja a kiválasztott csomópont melletti összes csomópontot. A BFS egyesével éri el ezeket a csomópontokat.
- A meglátogatott és megjelölt adatokat a BFS sorba rakja. A várakozási sor az első az első kimenetel alapján működik. Ezért az első, a grafikonba helyezett elemet először törlik, és ennek eredményeként kinyomtatják.
- A BFS algoritmus soha nem kerülhet végtelen hurokba.
- A nagy pontosságú és robusztus megvalósítás miatt a BFS-t számos valós megoldásban használják, például P2P-hálózatokban, Webrobotokban, és a hálózati műsorszórás.