A haranggörbe, más néven normál eloszlás, a leggyakoribb elosztási típus egy változó esetében. Olyan eloszlásként fogadják el, amely természetesen számos helyzetben előfordul. Haranggörbe esetén az ív legmagasabb pontja határozza meg az átlagot, amely egy elem előfordulásának legnagyobb száma. Az előfordulások valószínűsége csökken a görbe mindkét oldala felé. Haranggörbe segítségével összehasonlíthatja az előadásokat a szélsőségek kizárásával, vagy meghatározhatja az elvárásait azzal a lehetőséggel, hogy az eredmény a középponttól balra vagy jobbra eső tartományon belül helyezkedik el. Ebben az útmutatóban bemutatjuk, hogyan hozhat létre haranggörbét az Excel alkalmazásban, például egy valós használati eset forgatókönyvével.
Munkafüzet letöltése
Alapok
Csak az adatkészlet átlagára (átlagára) és a szórására van szükség. Mindkét mutató kiszámítható az Excelben az alábbi képletek segítségével.
E két érték figyelembevételével a normálisan elosztott értékek a következő szabályokat követik:
- A görbe egyenlő 1-vel (100%)
- A haranggörbe középpontja az adatpont átlaga
- (1-σ) A görbe alatti terület körülbelül 68,2% -a egy szórásba esik (átlag ± szórás)
- (2-σ) A görbe alatti terület körülbelül 95,5% -a két standard eltérésbe esik (átlag ± 2 * szórás)
- (3-σ) A görbe alatti terület körülbelül 99,7% -a három szóráson belül esik (átlag ± 3 * szórás)
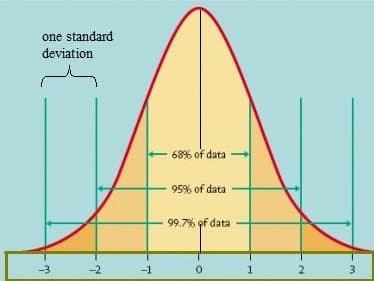
Kép a Virginia Egyetemről
Haranggörbe létrehozása az Excel-ben
Vegyünk egy közös példát, és mondjuk, hogy elemezzük a vizsgaeredményt lts egy tanulóosztály számára. Haranggörbét fogunk használni a vizsgaeredmények mérésére a jobb összehasonlítás érdekében.
A metrikák kiszámításával kezdjük a görbe generálásához szükséges normál elosztott adatokat. Számolnunk kell:
- Az értékek átlaga (átlaga).
- Az értékek szórása.
- 3-standard eltérési határértékek és az átlag után.
- Intervallumérték a normálisan elosztott adatpontokhoz. Ehhez az intervallumpontok meghatározása is szükséges. Bármelyik számot kiválaszthatja, de ezt ne feledje, a több intervallum nagyobb pontosságot jelent.
Metrika
Az adatok átlagának és szórásának kiszámításával kezdődik. Az AVEREAGE és az STDEV.P függvényekkel kiszámíthatja az átlag- és a szórásértékeket.

A következő lépés a számítás a 3 szórásérték az adatok 99,7% -ának minimális és maximális értékeinek beállításához.

Maximum = 83.23 – 3 * 5.54 = 99.86
Miután megadtuk a görbe minimum és maximum értékét, generálnunk kell az intervallumokat . Az intervallumértékek lesznek a normálisan elosztott értékek alapja. Az intervallumok kiszámításához mindössze annyit kell tennie, hogy elosztja a területet a minimális és maximális értékek között intervallumszámlálással. Ebben a példában ezt 20-ra állítottuk, de nagyobb számmal növelheti az adatpontok számát.

Az intervallumérték kiszámítása után létrehozhatja az adatpontokat. Ehhez írja be a minimális értéket egy cellába. Ezután közvetlenül a minimális érték alatt adja meg a képletet, hogy hozzáadja az intervallum értékét a minimumhoz. Itt cellahivatkozásokat használtunk (például J4-ként), amelyek segítenek az adatpontok könnyű feltöltésében a maximális értékig.

A következő lépés a normálisan elosztott értékek kiszámítása a létrehozott adatpontokból. Az Excel NORM.DIST függvényével létrehozhatja ezeket az értékeket.
A feltöltött adatpontokat használja a függvény első argumentumaként. A következő érvek az átlag és a szórás értékei. Fejezze be a képletet egy FALSE logikai értékkel a funkció nem kumulatív típusának használatához.

Diagram
Már majdnem kész! Válassza ki az adatpontokat és a normál eloszlási értékeket, majd helyezzen be egy X-Y szórásdiagramot. A Szórt sima vonalakkal változat segítségével hozzon létre haranggörbét az Excelben.

Úgy tűnik, hogy a diagram először kissé kikapcsol.Nézzük meg, hogyan teheti jobbá.
A diagram címének megváltoztatásához kattintson duplán a címre, és frissítse a nevet.
Ezután kattintson duplán a X tengely, és határozza meg a minimális és maximális értékeket az Axis Options panelen, hogy kiküszöbölje a kétoldalas fehér helyet. Ez jobbá teszi a diagram harang alakját. Olyan értékeket állítunk be, amelyek kissé kívül esnek az adathalmazunkon. Például 66 – 100 a 66,30 – 99,86 értékekhez.
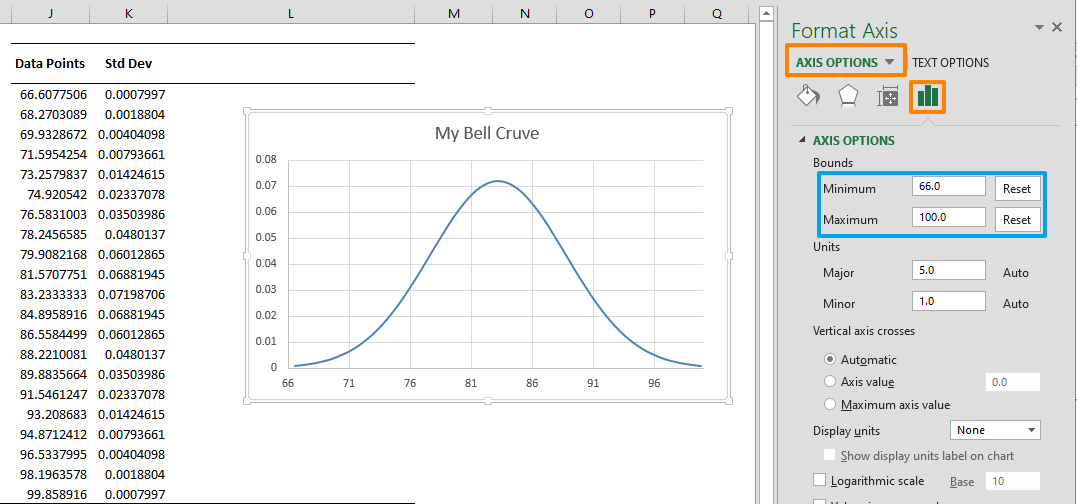
A diagramot tovább javíthatja a szórásértékek hozzáadásával .
