Bevezetés a k-legközelebbi szomszédokba: Nagy teljesítményű gépi tanulási algoritmus (megvalósítással a Python & R-ben)

Megjegyzés: Ezt a cikket eredetileg 2014. október 10-én tették közzé és 2018. március 27.

Áttekintés

• A k legközelebbi szomszéd (KNN) megértése – az egyik legnépszerűbb gépi tanulási algoritmus
• Ismerje meg a kNN működését a pythonban
• Válassza ki a k megfelelő értékét egyszerűbb kifejezésekkel

Bevezetés

A négy év alatt adattudományi pályafutásom során több mint 80% -os osztályozási modellt és csak 15-20% -os regressziós modellt építettem fel. Ezek az arányok többé-kevésbé általánosíthatók az egész iparágban. A besorolási modellek iránti elfogultság oka az, hogy a legtöbb analitikai probléma a döntés meghozatalával jár. digitális kampányok, függetlenül attól, hogy az ügyfelek nagy potenciállal rendelkeznek-e, stb. Ezek az elemzések átlátóbbak és közvetlenül kapcsolódnak a megvalósítás ütemtervéhez.

Ebben a cikkben egy másik széles körben alkalmazott gépi tanulási osztályozási technikáról fogunk beszélni, az úgynevezett K-legközelebbi szomszédok (KNN) néven. Elsősorban arra összpontosítunk, hogyan működik az algoritmus, és hogyan befolyásolja a bemeneti paraméter a kimenetet / előrejelzést.

Megjegyzés: Azok az emberek, akik szívesebben tanulnak videók segítségével, ugyanezt megtanulhatják az ingyenes tanfolyamunkon keresztül is – K- A legközelebbi szomszédok (KNN) algoritmusa a Pythonban és az R-ben. És ha Ön teljesen kezdő az adattudománynak és a gépi tanulásnak, nézze meg Certified BlackBelt programunkat –

• Certified AI & ML Blackbelt + program

Tartalomjegyzék

• Mikor használjuk a KNN algoritmust?
• Hogyan működik a A KNN algoritmus működik?
• Modellünk összehasonlítása a scikit-learn

Mikor használjuk a KNN algoritmust?

A KNN mindkét esetben használható osztályozás és regresszió prediktív problémák. Szélesebb körben használják azonban az ipar osztályozási problémáiban. Bármely technika értékeléséhez általában 3 fontos szempontot vizsgálunk meg:

1. Könnyen értelmezhető a kimenet

2. Számítási idő

3. Prediktív erő

Vegyünk néhány példát a KNN elhelyezésére a skálán:

A KNN algoritmusok a szempontok összes paraméterén át mutatnak be Általában könnyen értelmezhető és alacsony számítási idő miatt használják.

Hogyan működik a KNN algoritmus?

Vegyünk egy egyszerű esetet: értsd meg ezt az algoritmust. A következőkben a vörös körök (RC) és a zöld négyzetek (GS) terjedését mutatjuk be:

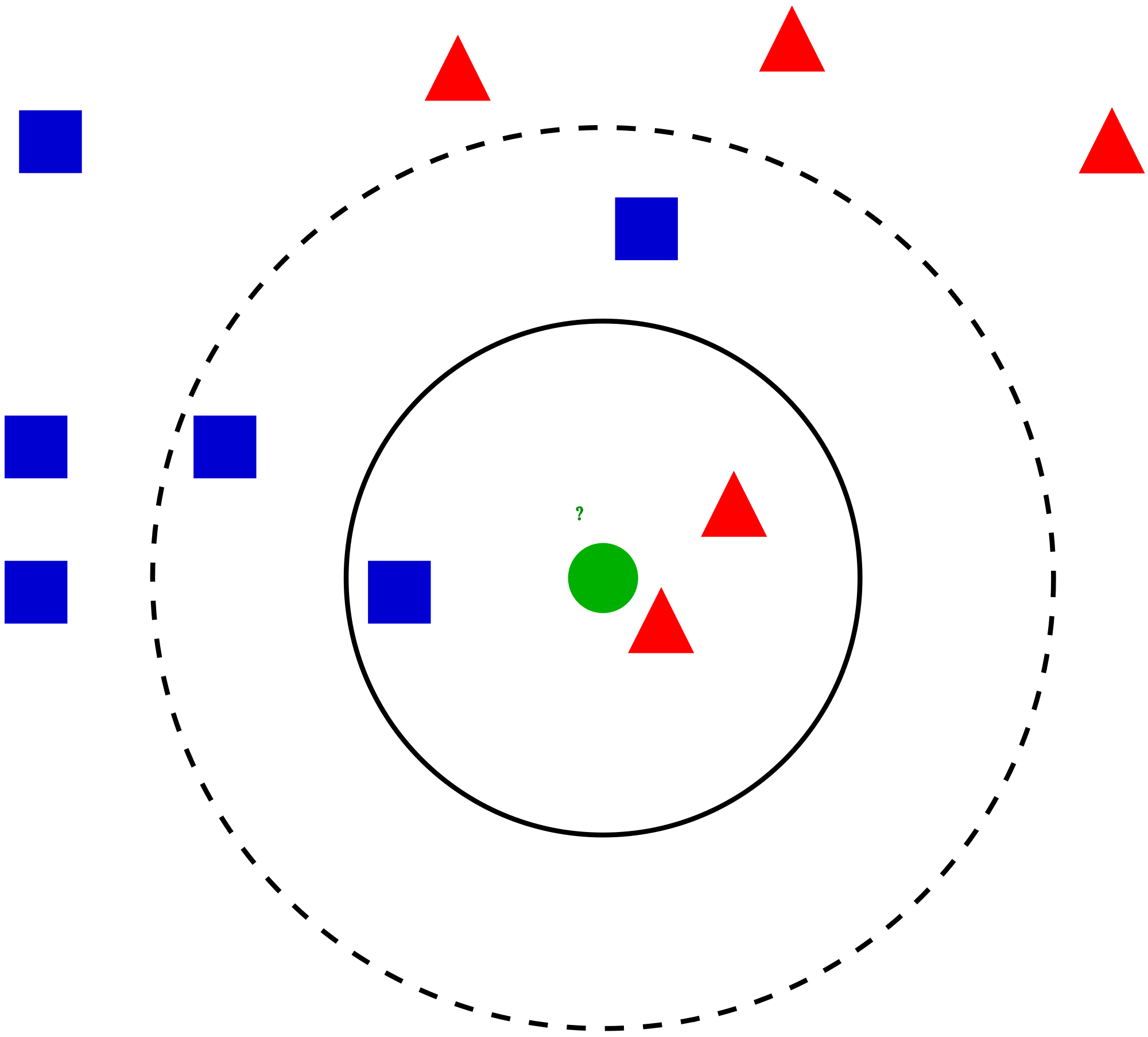
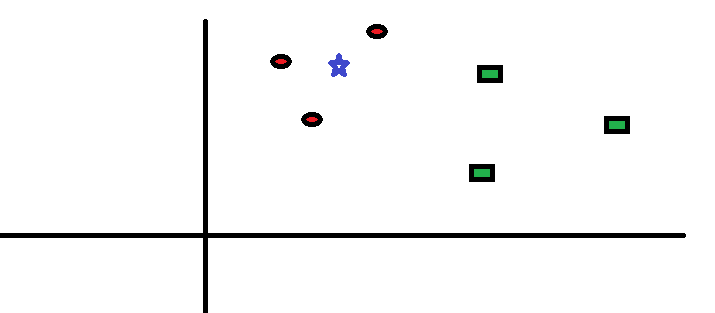Meg akarja találni a kék csillag osztálya (BS). A BS lehet RC vagy GS, és semmi más. A “K” KNN algoritmus a legközelebbi szomszéd, akitől a szavazatot el akarjuk venni. Tegyük fel, hogy K = 3. Ennélfogva most egy kört fogunk készíteni, amelynek középpontja BS, akkora, hogy csak három adatpontot csatol a síkra . További részletekért tekintse meg a következő ábrát:

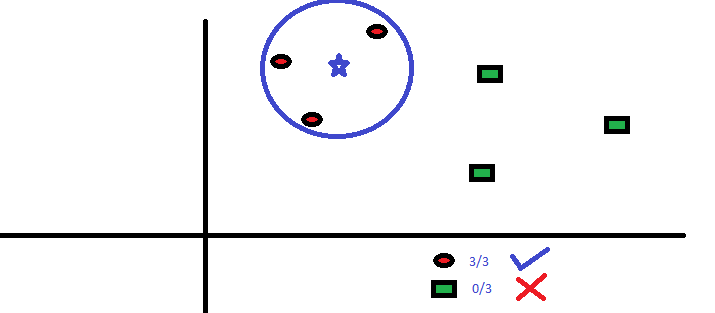A BS három legközelebb eső pontja mind RC, ezért jó magabiztossági szint mellett azt mondhatjuk, hogy a BS-nek az RC osztályba kell tartoznia. Itt a választás nagyon nyilvánvalóvá vált, mivel a legközelebbi szomszéd mindhárom szavazata RC-re ment. A K paraméter kiválasztása nagyon fontos ebben az algoritmusban . Ezután meg fogjuk érteni, melyek azok a tényezők, amelyeket figyelembe kell venni a legjobb K. megkötéséhez.

Hogyan válasszuk ki a K tényezőt?

Először próbáljuk megérteni, hogy pontosan mit is befolyásol a K az algoritmusban. Ha az utolsó példát látjuk, tekintettel arra, hogy mind a 6 edzésmegfigyelés állandó marad, egy adott K értékkel megadhatjuk az egyes osztályok határait. se határok elválasztják az RC-t a GS-től. Ugyanígy próbáljuk meglátni a “K” értéknek az osztályhatárokra gyakorolt hatását. Az alábbiakban bemutatjuk azokat a különböző határokat, amelyek elválasztják a két osztályt a K különböző értékeivel.

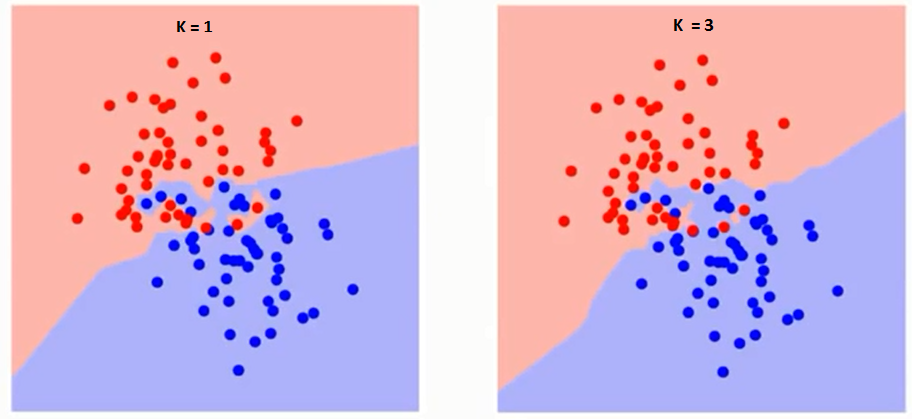
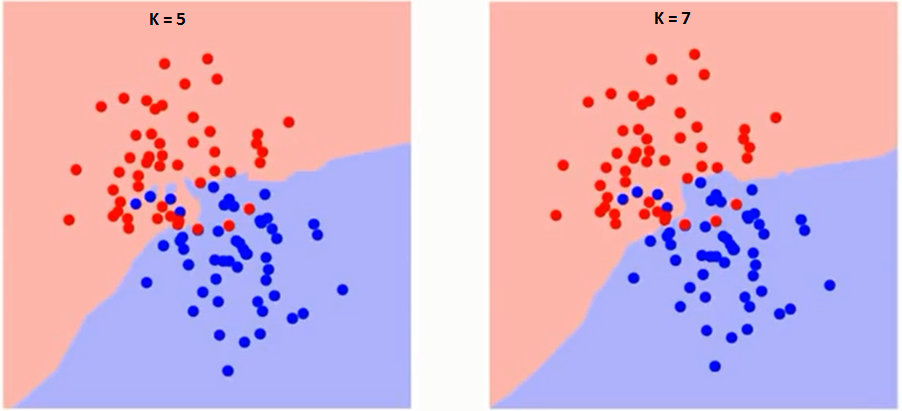
Ha figyelmesen figyel, láthatja, hogy A K értékének növekedésével a határ simábbá válik. A K végtelenségig növekvő értéke végül a teljes többség függvényében teljesen kék vagy vörös lesz. Az edzés hibaaránya és az érvényesítési hibaarány két paraméter, amelyekhez különböző K-értékeket kell elérnünk. Az alábbiakban látható a változó K értékű edzés hibaarányának görbéje:

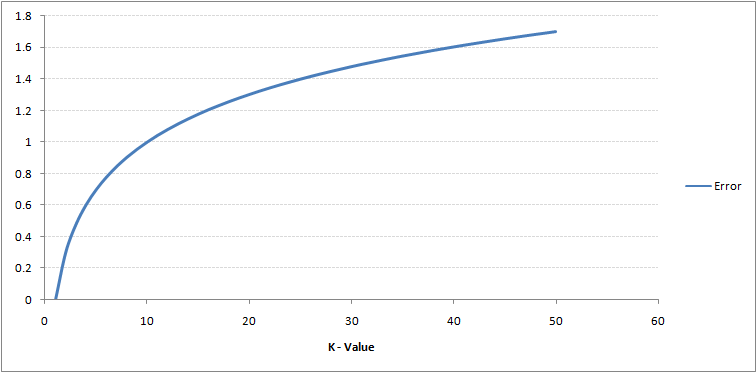Mint látható, a a hibaarány K = 1-nél mindig nulla a képzési mintához.Ennek az az oka, hogy az edzés adatpontjának a legközelebbi pontja maga. Ezért az előrejelzés mindig pontos K = 1 esetén. Ha az érvényesítési hiba görbéje hasonló lett volna, akkor a K választásunk 1 lett volna. Ezután következik az érvényesítési hiba görbe változó K értékkel:

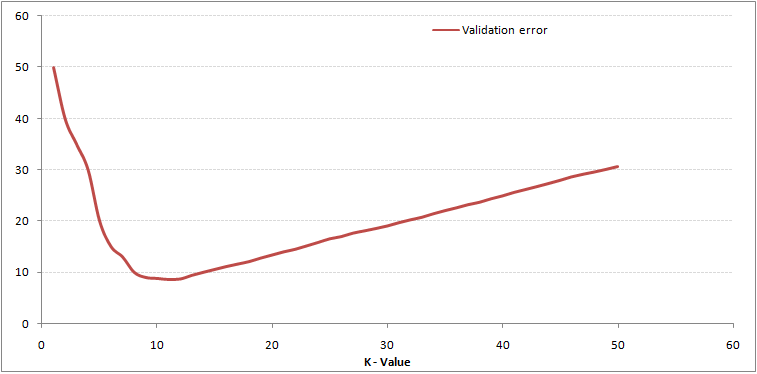Ez világosabbá teszi a történetet. K = 1-nél túlléptük a határokat. Ezért a hibaarány kezdetben csökken és eléri a minimumokat. A minimum pont után ez a K. növekedésével növekszik. A K optimális értékének megszerzéséhez elkülönítheti a képzést és az érvényesítést a kezdeti adatkészlettől. Most ábrázolja az érvényesítési hiba görbét a K optimális értékének megszerzéséhez. Ezt a K értéket minden előrejelzésnél fel kell használni. KNN) Algoritmus a Pythonban és az R

lebontása – KNN álkód

A KNN modellt az alábbi lépések végrehajtásával valósíthatjuk meg:

1. Töltse be az adatokat
2. Inicializálja a k értékét
3. A megjósolt osztály megszerzéséhez iteráljon 1-től az edzés adatpontjainak teljes számáig
   1. Számítsa ki a teszt közötti távolságot adatok és az edzés minden egyes sora. Itt az euklideszi távolságot fogjuk használni távolságmérőként, mivel ez a legnépszerűbb módszer. A többi használható mutató a Chebyshev, a koszinusz stb.
   2. Rendezze a kiszámított távolságokat növekvő sorrendbe a távolságértékek alapján
   3. Szerezzen be legfelső k sort a rendezett tömbből
   4. E sorok leggyakoribb osztályának megszerzése
   5. Visszaadja az előre jelzett osztályt

A Python implementációja a semmiből

A KNN modell felépítéséhez a népszerű Iris adatkészletet fogjuk használni. Innen töltheti le.

Modellünk összehasonlítása a scikit-learn

Láthatjuk, hogy mindkét modell ugyanazt az osztályt jósolta (Iris- virginica ) és ugyanazok a legközelebbi szomszédok (). Ezért megállapíthatjuk, hogy modellünk a várt módon működik.

A kNN megvalósítása az R

1. lépés: Az adatok importálása

2. lépés: Az adatok ellenőrzése és az adatok összegzésének kiszámítása

Kimenet

3. lépés: Az adatok felosztása

4. lépés: Számítás az euklideszi távolság

5. lépés: A függvény megírása a kNN előrejelzéséhez

6. lépés: K = 1 címke (név) kiszámítása

Kimenet

For K=1 "Iris-virginica"

Ugyanígy kiszámíthatja a K egyéb értékeit is.

A kNN prediktor függvény összehasonlítása az “Osztály” könyvtárral

Kimenet

For K=1 "Iris-virginica"

Láthatjuk, hogy mindkettő a modellek ugyanazt az osztályt jósolták (Iris-virginica).

Végjegyzetek

A KNN algoritmus az egyik legegyszerűbb osztályozási algoritmus. ilyen egyszerűséggel rendkívül versenyképes eredményeket hozhat. A KNN algoritmus regressziós problémákra is használható. A tárgyalt módszertan szerint a legközelebbi szomszédok átlagainak felhasználása lesz a legközelebbi szomszédok szavazása helyett. A KNN egyetlen sorban kódolható az R-n. Még nem kell feltárnom, hogyan használhatnánk a KNN algoritmust az SAS-on.

Hasznosnak találta a cikket? Használtál más gépi tanulási eszközt a közelmúltban? Tervezi-e használni a KNN-t üzleti problémáiban? Ha igen, ossza meg velünk, hogyan tervezi ezt folytatni.

Ha tetszik az imént olvasott & szeretné folytatni az elemzés tanulását, iratkozzon fel a e-maileket, kövessen minket a twitteren, vagy lájkolja a facebook oldalunkat.