Hogyan változik a nyomás a térfogat változásától az ideális gáz adiabatikus tágulása és sűrítése során? Ez az oldal a hangbeszélgetésünk melléklete. A légköri nyomáson lévő levegő majdnem ideális gáz, és a levegőben lévő hangátvitel normál frekvenciákhoz és átviteli távolságokhoz közel adiabatikus. (Az alábbiakban visszatérünk erre a feltételezésre.)
A termodinamika első törvénye a belső energia dU változását a rendszer által elvégzett dW munkához és a hozzá adott dQ hőhöz viszonyítja.
dU = dQ – dW
Definíció szerint egy adiabatikus folyamatban a hőcserélődött dQ = 0. Ennek behelyettesítése az első törvénybe és átrendezés
0 = dQ = dU + dW
A második kifejezés egyszerű: a dW elvégzett munka, amikor egy rendszer dV által megváltoztatja az V térfogatát, PdV.
Az első kifejezés kapcsolódhat a fajlagos hőhöz, amelyet az egység mol hőmérsékletére eső egységnyi hőmérséklet-változásonként hozzáadott hőként határozunk meg. Ha állandó térfogatú hőt adunk hozzá, akkor a gáz nem tágul, és így nem működik. Tehát a hozzáadott hő növeli a belső U energiát. Tehát ebből a definícióból következik, hogy az állandó térfogatú fajlagos hő ![]() , ahol n az anyajegyek száma. Ezért
, ahol n az anyajegyek száma. Ezért
Most egy ideális gáz állapotegyenlete
nRT = PV ( ii)
ahol R a gázállandó. Származékokat véve
Kombinálhatjuk az (i) és (iii) egyenleteket a T (i) kiküszöbölésére és (ii) adja meg ezeket a kifejezéseket az ncv dT esetében:
A PdV és VdP kifejezések összegyűjtése
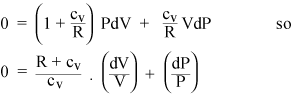
Ha a gáz ideális, akkor a belső energiája mind kinetikus, tehát az U belső energia csak T-től függ. Az ideális gáz (ii) állapotegyenletéből kiszámíthatjuk az állandó nyomáson végzett dW munka: ez csak PdV = nRdT. Tehát, ha állandó nyomáson adunk hőt egy gázhoz, akkor minden gázmólra fel kell melegítenünk az RdT-t, a hőn túl pedig állandó térfogatban kell adnunk. Tehát az ideális gáz fajlagos hője állandó nyomáson csak cP = cv + R. A fajlagos melegek aránya szabványos szimbólumot kap:
. Tehát van
(iv)
Ez az a fő eredmény, amelyre a hanghullámok megvitatásához szükségünk van: most megmutattuk, hogy a nyomás arányos változása γ-szorosa a térfogat arányos változásának vagy γ-szorosa a sűrűség arányos változásának. >
Ne álljunk meg itt, mert csak néhány sort választunk el egy fontos eredménytől. Tudjuk, hogy d (ln x) = dx / x (a bizonyítást lásd a számológépben). Tehát írhatunk az előző egyenlet
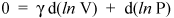
és átrendezheti, hogy megkapja
(v)
Ezért adiabatikus folyamat ideális gázban,
. (vi)
Elmélkedéskor elfogadja, hogy a cP > cV: At állandó térfogat, minden th Az Ön által betöltött hő a belső energia növelésére és a hőmérséklet emelésére szolgál. Állandó nyomáson nemcsak a belső energiát megemelő hőt kell betöltenie, hanem egy olyan hőmennyiséget is, amely megegyezik az elvégzett munkával, amikor a rendszer hőtáguláson megy keresztül. Levegő esetén γ körülbelül 1,4.
Természetesen most helyettesíthetjük a (vi) kifejezésre az (ii) állapotegyenletből, hogy lássuk, hogyan kapcsolódnak P és T, illetve T és V egy adiabatikus folyamathoz.
Mikor adiabatikus a hang?
Fentebb említettük, hogy “a levegőben történő hangátvitel normál frekvenciák és átviteli távolságok közelében közel van az adiabatikához”. Mikor nem sikerül? Hanghullámban a nyomásmaximumnál a hőmérséklet magas. Tehát arra számítunk, hogy némi hő diffundál a szomszédos nyomásminimumokhoz. Természetesen a hanghullám félperiódusában nincs sok idő a fél fél hullámhossz diffundálására. A hő diffundálódásához szükséges idő azonban a távolság négyzetének felel meg. Tehát ez a folyamat kevésbé elhanyagolható a magas frekvenciák esetében, mert a rövidebb fél hullámhossz több, mint kompenzálja a rövidebb félperiódust. Ez a diffúzió kiveszi a mechanikai energiát a hullámból, különösen nagy frekvenciák mellett, és a hatás az átviteli távolsággal növekszik.Emiatt (és néha mások) a távoli hangok nemcsak kevésbé hangosak, de kevésbé is fényesek, mint a közeli hangok.