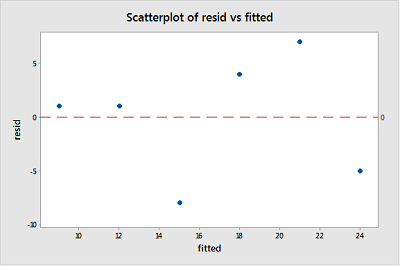
A maradványelemzés során a “maradványok versus illeszkedési cselekmény” a leggyakrabban létrehozott ábra. Ez egy maradványok szórási diagramja az y tengelyen és az illesztett értékek (becsült válaszok) az x tengelyen. A grafikont a nem-linearitás, az egyenlőtlen hibaváltozások és a kiugró értékek észlelésére használják.
Nézzünk meg egy példát, hogy nézzen ki egy “jól viselkedő” maradék cselekmény. Néhány kutató (Urbano- Marquez és munkatársai, 1989) érdekeltek voltak annak meghatározásában, hogy az alkoholfogyasztás lineárisan kapcsolódik-e az izomerőhöz. A kutatók egy n = 50 alkoholista férfi véletlenszerű mintáján mérték az alkohol (x) teljes életfogyasztását. a deltoid izom ereje (y) minden ember nem domináns karjában. A kapott adatok illesztett vonaldiagramja (alkoholarm.txt) a következőképpen néz ki:
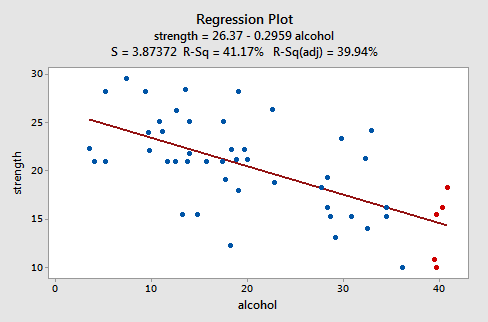
A cselekmény arra utal, hogy csökken az lineáris kapcsolat az alkohol és a kar ereje között. Azt is sugallja, hogy az adatkészletben nincsenek szokatlan adatpontok. Ez azt is szemlélteti, hogy a becsült regressziós vonal körüli variáció állandó, ami azt sugallja, hogy az egyenlő hibaváltozások feltételezése ésszerű. egyszerű lineáris regressziós modell, amelynek karja a válasz és az alkoholfogyasztás előrejelzője:
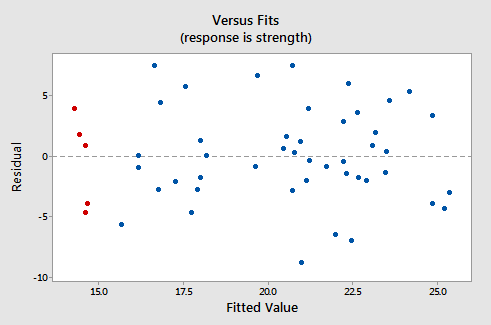
Ne feledje, hogy a maradék az definíció szerint az y tengelyen, az illesztett értékek pedig az x tengelyen jelennek meg. Vissza kell tudnia nézni az adatok szóródási diagramját, és meg kell néznie, hogy az ott lévő adatpontok hogyan felelnek meg az itt lévő maradvány és illeszkedés ábrán szereplő adatpontoknak. Ha problémája adódna ezzel, akkor nézze meg az eredeti szórási diagram öt piros pontját. Vegye figyelembe, hogy ezeknek a férfiaknak (akiknek alkoholfogyasztása 40 körül van) várható válasza (illesztett értéke) körülbelül 14 Ezenkívül vegye figyelembe azt a mintát, amelyben az öt adatpont eltér a becsült regressziós vonaltól.
Most nézze meg, hogy ez az öt adatpont hogyan és hol jelenik meg a maradék kontra illeszkedési diagramban. Illesztett értéke körülbelül 14 és a maradék = 0 vonaltól való eltérésük megegyezik a becsült regressziós vonaltól való eltérésükkel. Látja-e a kapcsolatot? Bármely adatpont, amely közvetlenül a becsült regressziós egyenesre esik, maradványa 0. Ezért a maradék = A 0 vonal megfelel a becsült regressziós vonalnak.
Ez a diagram a jól viselkedő maradványok és illeszkedések ábrájának klasszikus példája. Íme a jól viselkedett maradvány és illeszkedési cselekmény jellemzői és azok javasolják az egyszerűek megfelelőségét e lineáris regressziós modell:
- A maradványok “véletlenszerűen ugrálnak” a 0 vonal körül. Ez arra utal, hogy ésszerű a feltételezés, hogy a kapcsolat lineáris.
- A maradványok nagyjából “vízszintes sávot” alkotnak a 0 vonal körül. Ez azt sugallja, hogy a hibakifejezések szórása egyenlő.
- Egyetlen maradvány sem “tűnik ki” a maradványok alapvető véletlenszerű mintázatából. Ez azt sugallja, hogy nincsenek kiugró értékek.
Általában azt szeretné, ha a maradék és illeszkedési parcellák a fenti cselekményhez hasonlítanának. Ne felejtsd el, hogy ezeknek a cselekményeknek az értelmezése szubjektív. Tapasztalatom az, hogy a maradványelemzést először tanuló hallgatók hajlamosak túlértelmezni ezeket a cselekményeket, minden fordulatot és fordulatot valami potenciálisan zavarónak tekintenek. Különösen vigyázzon arra, hogy túl nagy súlyt helyezzen a maradék vs. illeszkedési parcellákra kis adatkészletek alapján. Előfordul, hogy az adatkészletek túl kicsiek ahhoz, hogy a maradványok és illeszkedési cselekmények értelmezését érdemes legyen megtenni. Ne aggódjon! Meg fogja tanulni – gyakorlással -, hogyan kell ezeket a cselekményeket “elolvasni”.