Tegyük fel, hogy a levegőt egy sima kerek csövön szivattyúzzák le, amelynek átmérője állandó, kivéve a középső szakaszt, ahol a cső keskenyedik az átmérő feléig, majd ismét kiszélesedik. Tegyük fel, hogy az átmérő minden változása simán megy végbe, és a levegő egyenletesen áramlik lefelé a csőben, örvény és turbulencia nélkül.
Gyakoroljon
a csőben hol várja a legnagyobb nyomás?
Válasz
A legtöbb ember ezt kérdezte először, és azt jósolja, hogy a nyomás a cső keskeny részén lesz a legnagyobb. De valójában, ha valóban elvégezzük a kísérletet, úgy, hogy nyomásmérőket helyezünk el a cső különböző pontjain, intuitív módon ellensúlyozzuk, hogy a légnyomás a legalacsonyabb ott, ahol a levegő a leggyorsabban mozog!

Hogy lássuk, hogy lehet ez, alkalmazzuk az általunk kifejlesztett technikák annak megállapítására, hogy a nyomás hogyan változik egy álló folyadékban. Emlékezzünk arra, hogy ezt úgy csináltuk, hogy egy kis hengerfolyadék szabad testdiagramját rajzoltuk meg. Mivel ez a kis henger nyugalomban volt, a teljes erő nulla volt, így a nettó nyomás kiegyenlítette a súlyt. Most vegyen figyelembe egy folyamatosan mozgó folyadékot. Hasznos az áramlás vizualizálása áramvonalak, vonalak rajzolásával úgy, hogy azok iránya az az irány legyen, amelyben a folyadék az egyes pontokban halad.

Valójában ezek az áramvonalak nemcsak azt mondják meg, hogy milyen irányban halad a folyadék, hanem képet adnak a sebességről is – ahol közelebb kerülnek egymáshoz, a folyadéknak gyorsabban kell haladnia, mert ugyanolyan mennyiségű folyadék áramlik szűkebb régión keresztül. Képzelje el, hogy most egy henger levegő mozog a cső mentén, tengelye párhuzamos az áramvonalral. Nyilvánvalóan fel kell gyorsulnia, amikor belép a cső keskeny részébe – mivel ugyanolyan mennyiségű levegő áramlik át a keskeny részen, mint a széles rész, akkor gyorsabban kell haladnia.
De ha a kicsi a folyadékhenger gyorsul, hátulról toló erővel kell hatni rá.
A súlya itt lényegtelen, mivel vízszintesen mozog. Ezért az egyetlen rá ható erő a nyomás, és arra a következtetésre kell jutnunk, hogy a hátsó nyomás nagyobb, mint az elülső nyomás. Ezért a keskeny részbe való belépéskor csökkennie kell a nyomásnak. Annak tisztázása érdekében, hogy mi történik, egy meglehetősen nagy hengert rajzolunk:
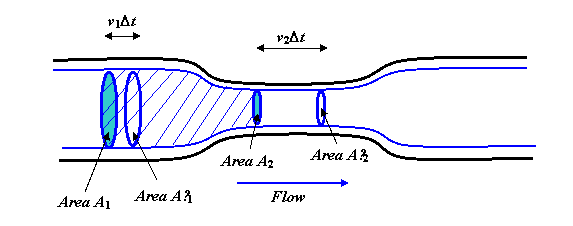
A folyadék folyamatosan és simán áramlik a pipa. A vastag kék vonalak áramvonalak, sőt, el kell képzelni, hogy az egész diagramot a központi tengely körül elforgatják, hogy háromdimenziós képet kapjanak, és a kék vonalak hengerré válnak, keskenyebb “nyak” szelettel, visszhangozva a cső.
Most vegye figyelembe a folyadéktestet a bemutatott áramvonalakon belül, és zárja le a két végét az A1 és A2 kör alakú területekkel. Az A1 folyadék áramlási sebességének meg kell egyeznie az áramlási sebességgel áramlik át az A2-n, mert egyenletes áramlásban a folyadék nem halmozódhat fel a közepén (vagy onnan sem merülhet ki). Az A1 alatt egy másodperc alatt átfolyó térfogat v1A1. (Ennek érdekében képzeljen el egy hosszú, egyenes csövet keskeny, Ha a folyadék áramlik, mondjuk másodpercenként 3 méterrel, akkor egy másodperc alatt átfolyik az összes folyadék, amely 3 méteren belül volt az A1 területtől az áramlási oldalon.)
Tehát, az A1 keresztmetszet megegyezik az A2 keresztmetszetével, \
(lábjegyzet: Talán érdemes megemlíteni, hogy implicit módon feltételezzük a veloci ty azonos az A1 terület minden pontján. Minden valódi folyadéknak van némi viszkozitása (súrlódása), és lassabban fog mozogni a cső oldalai közelében, mint a közepén. Ezt később megbeszéljük. Egyelőre “ideális” folyadéknak tekintjük azt a kifejezést, amelyet akkor használunk, ha figyelmen kívül hagyjuk a viszkozitást. Valójában a kapott eredmény rendben van – egy apró A1 területet vehettünk volna el az oldalaktól, így a sebesség ugyanez az egész területre, de ez sokkal kevésbé világos diagramot adott volna.)
Most már készen állunk megvizsgálni a folyadék kinetikus energiájának növekedését, amikor az felgyorsul a keskeny részre, és értsd meg, hogy a nyomáskülönbség hogyan végezte el a felgyorsításához szükséges munkát.
\
Az energia növekedésének egyetlen lehetséges forrása az a nyomás által végzett munka, amely a folyadékot a a keskeny rész.
\
Tehát ez a folyadékdarabunkon végzett munka azáltal, hogy a folyadék tolja hátulról – de ezzel még nem ért véget a történet, mert a A folyadék maga úgy működik, hogy a folyadékot maga elé tolja, ezért, hogy megtalálja a darabunk energiájának teljes növekedését, le kell vonni a külső munkát.Vagyis a folyadékunkra gyakorolt nyomás által végzett teljes munka
\
erre emlékezve \ (A_1v_1 = A_2v_2 \).
Ennek az elvégzett munkának egyenlőnek kell lennie a kinetikus energia változása, ezért
\
amelyből
\
Ez Bernoulli egyenlete.
\.
Közreműködők és hozzárendelések
- Michael Fowler (gerendák professzor, Virginia Egyetem Fizika Tanszéke)