 |
Un cercle est facile à faire: Tracez une courbe à « rayon » Et ainsi: Tous les points sont à la même distance du centre. |

Vous pouvez le dessiner vous-même
Mettez une épingle dans un tableau, mettez une boucle de ficelle autour delle et insérez un crayon dans la boucle. Gardez la chaîne étirée et dessinez le cercle!
Jouez avec
Essayez de faire glisser le point pour voir comment le rayon et la circonférence changent.
(Voyez si vous pouvez continuer un rayon constant!)
Rayon, diamètre et circonférence

Le rayon est la distance du centre vers lextérieur.
Le diamètre va directement à travers le cercle, à travers le centre.
La circonférence est la distance une fois autour du cercle.
Et voici la chose vraiment cool:
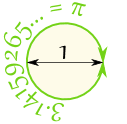
Lorsque nous divisons la circonférence par le diamètre, nous obtenons 3,141592654 …
qui est le nombre π (Pi)
|
Ainsi, lorsque le diamètre est 1, la circonférence est 3,141592654 … |
 |
On peut dire:
Circonférence = π × Diamètre
Exemple: Vous marchez autour dun cercle de 100 m de diamètre, jusquoù avez-vous parcouru?
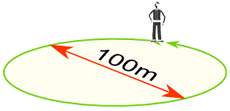
Distance parcourue = Circonférence = π × 100m
= 314m (au m le plus proche)
Notez également que le diamètre est deux fois le rayon:
Diamètre = 2 × Rayon
Et cest aussi vrai:
Circonférence = 2 × π × Radius
En résumé:
| × 2 | × π |
| |
|
| Rayon | Diamètre | Circonférence |
Se souvenir
La longueur des mots peut vous aider à vous souvenir:
- Rayon est le mot le plus court et le plus court est mesure
- Le diamètre est plus long
- La circonférence est la plus longue
Définition
 |
Le cercle est une forme plane (bidimensionnelle), donc: |
Cercle: lensemble de tous les points sur un plan qui sont à une distance fixe dun centre.
Aire

Laire dun cercle est égale à π fois le rayon au carré, qui est écrit:
A = π r2
Où
- A est la zone
- r est le rayon
Pour vous aider à vous souvenir de penser « Les tartes sont au carré » (même si les tartes sont généralement rondes):

Exemple: Quelle est laire dun cercle de rayon de 1,2 m?
Ou, en utilisant le diamètre:

A = (π / 4) × D2
Aire comparée à un carré

Un cercle a environ 80% de laire dun carré de largeur similaire.
La valeur réelle est (π / 4) = 0,785398 .. . = 78.5398 …%
Et quelque chose dintéressant pour vous:
Voir Circle Area by Lines
Noms
Parce que les gens ont des cercles étudiés depuis des milliers dannées, des noms spéciaux sont apparus.
Personne ne veut dire « cette ligne qui commence dun côté du cercle, passe par le centre et se termine de lautre côté » alors quils peuvent simplement dites « Diamètre ».
Voici donc les noms spéciaux les plus courants:
Lignes

Une ligne qui » touche simplement « le cercle en passant sappelle une tangente.
Une ligne qui coupe le cercle en deux points est appelée une sécante.
Un segment de ligne qui va dun point à un autre sur la circonférence du cercle est appelé un accord.
Sil passe à travers le centre, on lappelle un diamètre.
Et une partie de la circonférence sappelle un arc.

Tranches
Il y a deux « tranches » principales dun cercle.
La tranche « pizza » sappelle un secteur.
Et la tranche formée par un accord sappelle un segment.
Secteurs communs
Le quadrant et le demi-cercle sont deux types spéciaux de secteur:

Un quart de cercle est appelé un quadrant.

Un demi-cercle est appelé un demi-cercle.
Intérieur et extérieur

Un cercle a un intérieur et un extérieur (bien sûr!). Mais il a aussi un « on », car nous pourrions être juste sur le cercle.
Exemple: « A » est à lextérieur du cercle, « B » est à lintérieur du cercle et « C » est sur le cercle .

Ellipse
Un cercle est un « cas particulier » dune ellipse.