Theveninin lause toteaa, että mikä tahansa monimutkainen lineaarinen piiri on mahdollista yksinkertaistaa vastaavaksi piiriksi, jossa on vain yksi jännitelähde ja sarjaan kohdistuva vastus kuormitukseen. ”Lineaarisen” määrittely on identtinen superpositiolauseen kanssa, jossa kaikkien taustalla olevien yhtälöiden on oltava lineaarisia (ei eksponentteja tai juuria) .Jos kyseessä on passiiviset komponentit (kuten vastukset ja myöhemmin, induktorit ja kondensaattorit ), on totta. On kuitenkin joitain komponentteja (varsinkin tietyt kaasupurkaus- ja puolijohdekomponentit), jotka ovat epälineaarisia: toisin sanoen niiden vastustusta jännitteen ja / tai virran nykyisiin muutoksiin. komponenttityypit, epälineaariset piirit.
Theveninin lause sähköjärjestelmissä
Theveninin lause on erityisen hyödyllinen analysoitaessa sähköjärjestelmiä ja muita piirejä, joissa piirissä on yksi tietty vastus (kutsutaan ”kuormaksi”) ”Vastus) voi muuttua, ja piiri on laskettava uudelleen jokaisen kuormitusvastuksen koearvon kanssa sen läpi olevan jännitteen ja sen läpi kulkevan virran määrittämiseksi. Tarkastellaan vielä kerran esimerkkipiiriä:

Oletetaan, että päätämme nimetä R2 ”vastukseksi” Meillä on käytössämme jo neljä analyysimenetelmää (haaravirta, verkkovirta, Millmanin lause ja superpositiolause), joita käytetään määrittämään jännite R2: n ja R2: n kautta kulkevan virran välillä, mutta jokainen näistä menetelmistä on aikaa vievää. Kuvittele, että toistat minkä tahansa näistä menetelmistä uudestaan ja uudestaan saadaksesi selville, mitä tapahtuisi, jos kuormitusresistanssi muuttuisi (kuormitusvastuksen muuttaminen on hyvin yleistä sähköjärjestelmissä, koska useita kuormia kytketään päälle ja pois päältä tarpeen mukaan. Niiden rinnakkaisliitäntöjen kokonaisvastus muuttuu riippuen siitä, kuinka monta on kytketty kerrallaan). Tämä voi mahdollisesti edellyttää paljon työtä!
Thevenin Equivalent Circuit
Theveninin lause tekee tämän helpoksi poistamalla väliaikaisesti kuormitusvastuksen alkuperäisen piirin ja jäljellä olevan määrän pienentäminen vastaavaan ciriin cuit koostuu yhdestä jännitelähteestä ja sarjavastuksesta. Kuormitusresistanssi voidaan sitten liittää uudelleen tähän ”Thevenin-ekvivalenttipiiriin” ja suorittaa laskelmat ikään kuin koko verkko olisi vain yksinkertainen sarjapiiri:

…. Thevenin-muunnoksen jälkeen..
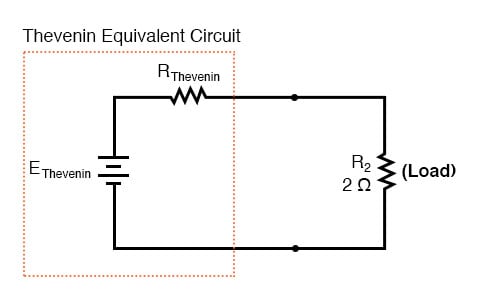
”Thevenin-ekvivalentti piiri” on B1: n, R1: n, R3: n ja B2: n sähköinen ekvivalentti, katsottuna kahdesta pisteestä, joihin kuormitusvastuksemme (R2) yhdistyy.
Thevenin-ekvivalenttipiiri, jos se on oikein johdettu, käyttäytyy täsmälleen samalla tavalla kuin alkuperäinen piiri, jonka muodostavat B1, R1, R3 ja B2. Toisin sanoen kuormitusvastuksen (R2) jännitteen ja virran tulisi olla täsmälleen samat saman piirin kuormitusvastuksen arvolle. Kuormitusvastus R2 ei voi ”erottaa B1: n, R1: n, R3: n ja B2: n alkuperäisen verkon ja ETheveninin ja RTheveninin Thevenin-ekvivalenttipiirin välillä edellyttäen, että ETheveninin ja RTheveninin arvot on laskettu oikein.
Etuna ”Thevenin-muunnoksen” suorittamisessa yksinkertaisemmaksi piiriksi on tietysti se, että se tekee kuormitusjännitteestä ja kuormavirrasta niin paljon helpommin ratkaistavissa kuin alkuperäisessä verkossa. Thevenin-lähdejännitteen ja sarjavastuksen ekvivalentin laskeminen on itse asiassa melko helppoa. Ensin valittu kuormavastus poistetaan alkuperäisestä piiristä, korvataan katkaisulla (avoin piiri):

Määritä Thevenin Jännite
Seuraavaksi määritetään jännite niiden kahden pisteen välillä, joihin kuormavastus oli aiemmin kiinnitetty. Käytä tähän käytettävissäsi olevia analyysimenetelmiä. Tässä tapauksessa alkuperäinen piiri kuormitusvastuksen ollessa irrotettuna ei ole muuta kuin yksinkertainen sarjapiiri vastakkaisten paristojen kanssa, joten voimme määrittää jännitteen avoimien kuormitusliittimien yli soveltamalla sarjapiirien sääntöjä, Ohmin lakia ja Kirchhoffin jännitettä Laki:

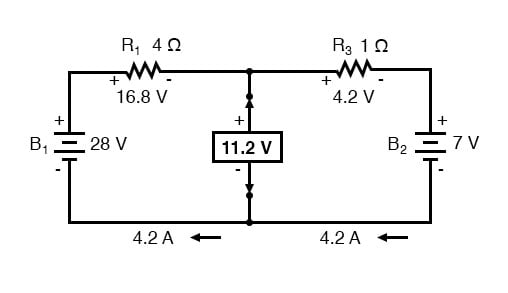
Jännite välillä kaksi kuormitusliitäntäkohtaa voidaan selvittää yhdestä akun jännitteestä ja toinen vastuksen jännitteestä laskee ja tulee 11,2 volttiin.Tämä on ”Thevenin-jännite” (EThevenin) vastaavassa piirissä:

Määritä Thevenin-sarjan resistanssi
Jotta löydettäisiin Thevenin-sarjan resistanssi vastaavalle piirillemme, meidän on otettava alkuperäinen piiri (kuormavastuksen ollessa vielä irrotettuna), poistettava virtalähteet (samalla tyylillä kuin teimme superpositiolauseen kanssa: jännitelähteet korvattu johdot ja virtalähteet korvattu katkoksilla) ja määritä vastus kuormitusliittimestä toiseen:

Poistamisen kanssa Kahden pariston kohdalla tässä paikassa mitattu kokonaisvastus on yhtä suuri kuin R1 ja R3 rinnakkain: 0,8 Ω. Tämä on ”Thevenin-vastus” (RThevenin) vastaavalle piirille:

Määritä kuormitusvastuksen jännite
Kun liitäntäpisteiden väliin on kiinnitetty kuormitusvastus (2 Ω), voimme määrittää sen yli olevan jännitteen ja virta läpi ikään kuin koko verkko olisi vain yksinkertainen sarjapiiri:

Huomaa, että R2: n jännite- ja virtaluvut (8 volttia, 4 ampeeria) ovat identtisiä muiden analyysimenetelmien avulla löydettyjen kanssa. Huomaa myös, että Thevenin-sarjan resistanssin ja Thevenin-lähteen (yhteensä) jännite- ja virtaluvut eivät koske mitään alkuperäisen, monimutkaisen piirin komponentteja. Theveninin lause on hyödyllinen vain määritettäessä, mitä tapahtuu yhdelle verkon vastukselle: kuormalle.
Etuna on tietysti se, että voit nopeasti selvittää, mitä tapahtuisi yhdelle vastukselle, jos se olisi muu arvo kuin 2 Ω tarvitsematta käydä läpi paljon analyyseja uudelleen. Liitä vain tämä kuormitusvastuksen arvo Theveninin vastaavaan piiriin ja pieni sarjapiirilaskenta antaa sinulle tuloksen.
TARKASTELU:
- Theveninin lause on tapa pienentää verkko vastaavaksi piiriksi, joka koostuu yhdestä jännitelähteestä, sarjavastuksesta ja sarjakuormituksesta.
- Theveninin lauseen seuraavat vaiheet:
- Etsi Thevenin-lähteen jännite poistamalla kuormitusvastus alkuperäisestä piiristä ja laskemalla jännite avoimien liitäntäpisteiden yli, joissa kuormavastus aiemmin oli.
- Löydä Thevenin-vastus poistamalla kaikki alkuperäisen piirin virtalähteet (jännitelähteet oikosulussa) ja virtalähteet auki) ja avoimen kytkentäpisteen välisen kokonaisvastuksen laskeminen.
- Piirrä Thevenin-ekvivalentti piiri Thevenin-jännitelähteellä sarjassa Thevenin-resistanssin kanssa. Kuormitusvastus kiinnittyy uudelleen vastaavan piirin kahden avoimen pisteen väliin.
- Analysoi kuormitusvastuksen jännite ja virta sarjapiirien sääntöjen mukaisesti.
LIITTYVÄ TYÖPAIKKA:
- Thevenins, Nortons and Maximum Power Transfer Theorems -taulukko