A summa on summauksen tulos. Esimerkiksi lisäämällä arvot 1, 2, 3 ja 4 summa 10 kirjoitettu
 |
(1)
|
Summattuja numeroita kutsutaan lisäyksiksi tai joskus summaiksi. Summaoperaatio voidaan ilmoittaa myös käyttämällä pääomasigmaa, jonka ylä- ja alarajat on kirjoitettu ylä- ja alapuolelle, ja alla ilmoitettua indeksiä. Esimerkiksi yllä oleva summa voidaan kirjoittaa
 |
(2)
|
numeroluettelon summa toteutetaan summana.
Summa
 |
(3)
|
jossa kukin termi 
annetaan jollakin kiinteällä säännöllä (ts. 
on hyvin määriteltyä sekvenssiä) kutsutaan (äärelliseksi) sarjaksi, ja jos termien lukumäärä 
on ääretön, summaa kutsutaan loputtomaksi sarjaksi (tai usein vain ”sarjaksi”). Lomakkeen summa
 |
(4)
|
kutsutaan geometriseksi sarjaksi .
Sarjan lähentymisen ehdot voidaan määrittää Wolfram-kielellä SumConvergence-toiminnolla.
Yleinen äärellinen tehosumma
 |
(5)
|
voidaan antaa lausekkeella
 |
(6)
|
joka vastaa Faulhaberin kaavaa, jossa merkintä 
tarkoittaa määrää kysymys nostetaan sopivaan tehoon 
ja kaikki muodon 
ehdot korvataan vastaavilla Bernoullin numerot 
.
Hauska identiteetti J. Ziegenbeinille (pers. 19. kesäkuuta 2002) seuraa identiteetistä
 |
(7)
|
joka voidaan kirjoittaa
 |
(8)
|
Siksi 
voidaan kirjoittaa vastaavissa muodoissa
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
ja niin edelleen.
Nicomachuksen lause antaa utelias lausekkeen tehosummalle 
.
Erikoissummat sisältävät
 |
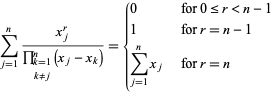(13)
|
ja
 |
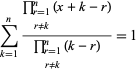(14)
|
Neliösarjan summan minimoimiseksi tiettyjen numeroiden lukumäärä 
tietystä numerosta 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
ota johdannainen.
 |
(17)
|
Ratkaisu kohteelle 
antaa
 |
(18)
|
joten 
minimoidaan, kun 
asetetaan tarkoittaa.