Johdatus k-lähimpiin naapureihin: tehokas koneoppimisalgoritmi (toteutettuna Python & R: ssä)

Huomaa: Tämä artikkeli julkaistiin alun perin 10. lokakuuta 2014 ja päivitettiin 27. maaliskuuta 2018

Yleiskatsaus

• Ymmärrä k lähin naapuri (KNN) – yksi suosituimmista koneoppimisalgoritmeista
• Opi kNN: n toiminta pythonissa
• Valitse oikea k: n arvo yksinkertaisella sanalla

Johdanto

Neljän vuoden aikana tietojenkäsittelyurastani olen rakentanut yli 80% luokitusmalleja ja vain 15-20% regressiomalleja. Nämä suhteet voivat olla enemmän tai vähemmän yleisiä koko toimialalla. Syy tähän luokittelumalleihin kohdistuvaan ennakkoluuloon on se, että useimpiin analyyttisiin ongelmiin liittyy päätöksen tekeminen.

Esimerkiksi, houkutteleeko asiakas vai ei, pitäisikö meidän kohdistaa asiakas X: hen digitaaliset kampanjat, riippumatta siitä, onko asiakkaalla suuri potentiaali vai ei. Nämä analyysit ovat oivaltavampia ja liittyvät suoraan toteutussuunnitelmaan.

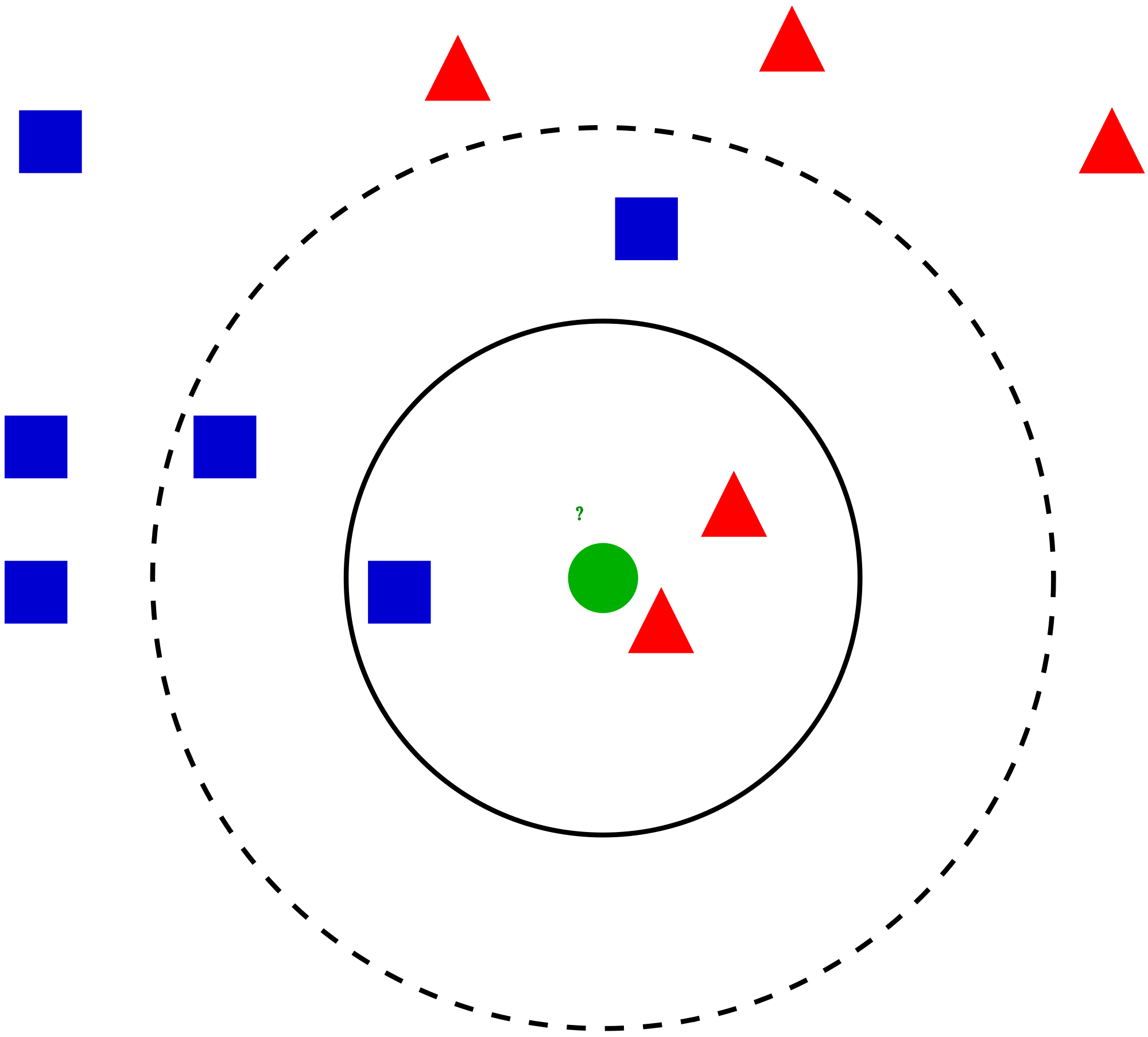
Tässä artikkelissa puhumme toisesta laajalti käytetystä koneoppimisen luokittelutekniikasta nimeltä K-lähimmät naapurit (KNN). Keskitymme ensisijaisesti siihen, miten algoritmi toimii ja miten syöttöparametri vaikuttaa tulokseen / ennakointiin.

Huomaa: Ihmiset, jotka haluavat oppia videoiden kautta, voivat oppia saman ilmaisen kurssimme kautta – K- Lähimmät naapurit (KNN) -algoritmi Pythonissa ja R.Ja jos olet täysin aloittanut datatieteen ja koneoppimisen, tutustu Certified BlackBelt -ohjelmaamme –

• Sertifioitu AI & ML Blackbelt + -ohjelma

Sisällysluettelo

• Milloin käytämme KNN-algoritmia?
• Kuinka KNN-algoritmi toimii?
• Kuinka valitaan tekijä K?
• Sen hajottaminen – KNN: n pseudokoodi
• Toteutus Pythonissa tyhjästä
• Mallimme vertaaminen scikit-learniin

Milloin käytämme KNN-algoritmia?

KNN: ää voidaan käyttää molempiin luokittelu ja regressioennustavat ongelmat. Sitä käytetään kuitenkin laajemmin alan luokitusongelmissa. Minkä tahansa tekniikan arvioimiseksi tarkastelemme yleensä 3 tärkeää näkökohtaa:

1. Helppo tulkita tulosta

2. Laskenta-aika

3. Ennakoiva voima

Otetaan muutama esimerkki KNN: n sijoittamiseksi asteikkoon:

KNN-algoritmi messuilla kaikilla näkökohdilla. Sitä käytetään yleisesti sen helposti tulkittavuuden ja matalan laskenta-ajan vuoksi.

Kuinka KNN-algoritmi toimii?

Otetaan yksinkertainen tapaus ymmärtää tämän algoritmin. Seuraavassa on punaisten ympyröiden (RC) ja vihreiden neliöiden (GS) leviäminen:

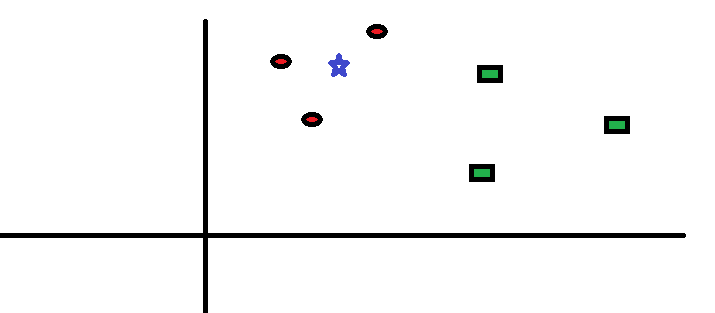Aiot selvittää sinisen tähden (BS) luokka. BS voi olla joko RC tai GS eikä mitään muuta. ”K” on KNN-algoritmi on lähin naapuri, jolta haluamme äänestyksen. Sanotaan K = 3. Siksi teemme nyt ympyrän, jonka keskipiste on BS, yhtä suuri kuin liitämme vain kolme datapistettä koneeseen . Katso lisätietoja seuraavasta kaaviosta:

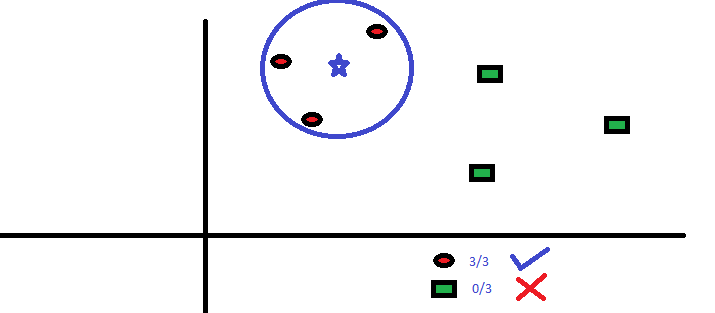BS: n kolme lähintä pistettä ovat kaikki RC. Hyvällä luotettavuustasolla voimme sanoa, että tukiaseman tulisi kuulua luokkaan RC.Tässä valinta tuli hyvin ilmeiseksi, koska lähimmän naapurin kaikki kolme ääntä menivät RC: lle. Parametrin K valinta on erittäin tärkeä tässä algoritmissa . Seuraavaksi ymmärrämme, mitkä tekijät on otettava huomioon parhaan K: n tekemisessä.

Kuinka valitaan kerroin K?

Yritetään ensin ymmärtää, mihin K tarkalleen vaikuttaa algoritmissa.Jos näemme viimeisen esimerkin, kun otetaan huomioon, että kaikki 6 harjoittelutarkkailua pysyvät vakioina, annetulla K-arvolla voimme tehdä kullekin luokalle rajat. Se rajot erottavat RC: n GS: stä. Yritetään samalla tavalla nähdä arvon ”K” vaikutus luokan rajoihin. Seuraavassa on eri rajat, jotka erottavat kaksi luokkaa eri arvoilla K.

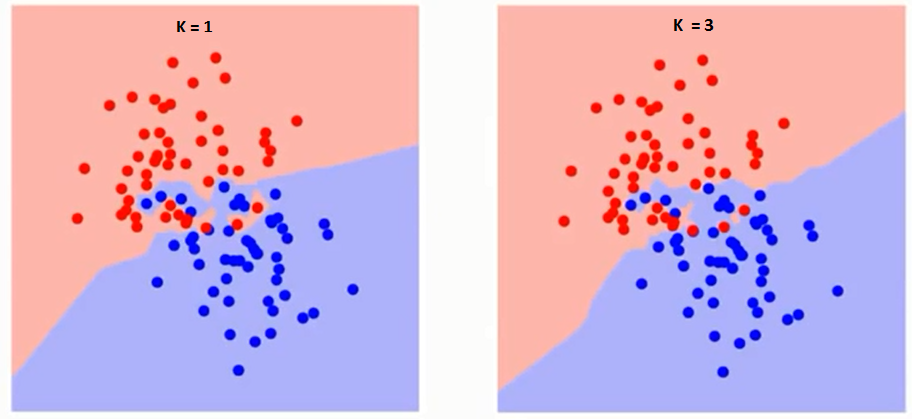
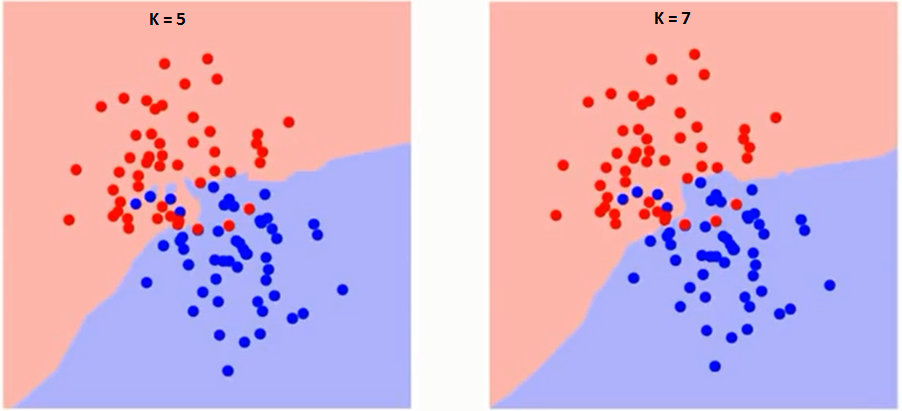
Jos katsot tarkkaan, näet sen Raja muuttuu tasaisemmaksi K: n arvon kasvaessa. Kun K kasvaa äärettömään, se muuttuu lopulta siniseksi tai punaiseksi kokonais enemmistön mukaan.Koulutuksen virhesuhde ja validointivirhesuhde ovat kaksi parametria, jotka meidän on käytettävä eri K-arvoon. Seuraavassa on käyrä harjoitteluvirheelle, jonka arvo vaihtelee K:

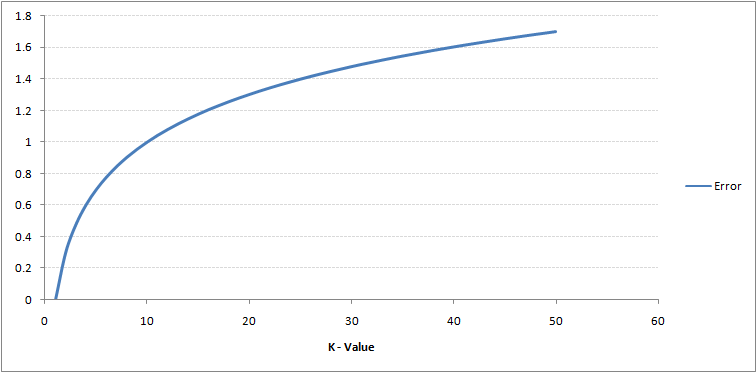Kuten näette, virhesuhde kohdassa K = 1 on aina nolla harjoitusnäytteelle.Tämä johtuu siitä, että minkä tahansa harjoituksen datapisteen lähin piste on itse, joten ennuste on aina tarkka, kun K = 1. Jos vahvistusvirhekäyrä olisi ollut samanlainen, valintamme K olisi ollut 1. Seuraavassa on vahvistusvirhekäyrä, jonka arvo vaihtelee K:

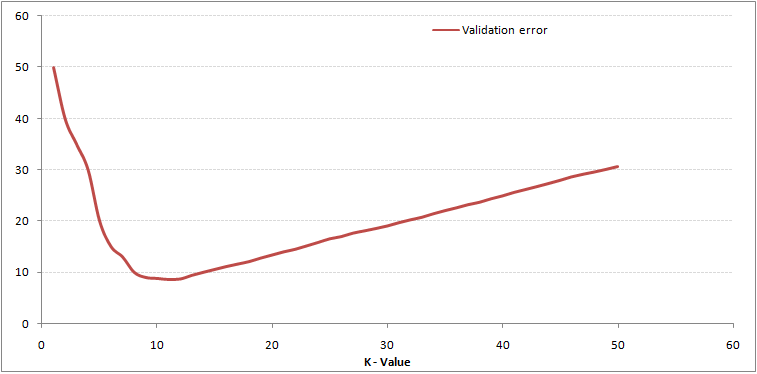Tämä tekee tarinasta selkeämmän. Kohdassa K = 1 olimme ylittämässä rajoja. Siksi virhesuhde aluksi pienenee ja saavuttaa minimit. Minimipisteen jälkeen se kasvaa K.: n kasvaessa. Saadaksesi optimaalisen K-arvon, voit erottaa harjoittelun ja validoinnin alkuperäisestä tietojoukosta. Piirrä nyt validointivirhekäyrä saadaksesi optimaalisen K.-arvon. Tätä K-arvoa tulisi käyttää kaikissa ennusteissa.

Yllä oleva sisältö voidaan ymmärtää intuitiivisemmin ilmaisen kurssimme – K-lähimmät naapurit ( KNN) Pythonin ja R: n algoritmi

Sen hajottaminen – KNN: n pseudokoodi

KNN-malli voidaan toteuttaa noudattamalla seuraavia vaiheita:

1. Lataa tiedot
2. Alusta k: n arvo
3. Ennustetun luokan saamiseksi iteroi 1: stä harjoittelun datapisteiden kokonaismäärään
   1. Laske testin välinen etäisyys tiedot ja jokaisen harjoitustietorivin. Tässä käytämme Euclidean etäisyyttä etäisyysmittarina, koska se on suosituin menetelmä. Muita mittareita, joita voidaan käyttää, ovat Chebyshev, kosini jne.
   2. Lajittele lasketut etäisyydet nousevassa järjestyksessä etäisyysarvojen perusteella
   3. Hanki k ylin rivi lajitellusta taulukosta
   4. Hanki näiden rivien yleisin luokka
   5. Palauta ennustettu luokka

Pythonin toteutus tyhjästä

Käytämme suosittua Iris-tietojoukkoa KNN-mallimme rakentamiseen. Voit ladata sen täältä.

Mallin vertaaminen scikit-learn

Voimme nähdä, että molemmat mallit ennustivat samaa luokkaa (Iris- virginica ) ja samat lähimmät naapurit (). Siksi voimme päätellä, että mallimme toimii odotetulla tavalla.

kNN: n käyttöönotto R: ssä

Vaihe 1: Tietojen tuominen

Vaihe 2: Tietojen tarkistaminen ja datan yhteenvedon laskeminen

Tulos

Vaihe 3: Tietojen jakaminen

Vaihe 4: Laskeminen euklidinen etäisyys

Vaihe 5: Funktion kirjoittaminen kNN: n ennustamiseksi

Vaihe 6: K = 1 -tunnisteen (nimi) laskeminen

Tulos

For K=1 "Iris-virginica"

Samalla tavalla voit laskea K: n muille arvoille.

Verrataan kNN-ennakointitoimintoa ”Luokka” -kirjastoon

Tulos

For K=1 "Iris-virginica"

Voimme nähdä, että molemmat mallit ennustivat saman luokan (Iris-virginica).

Loppuhuomautukset

KNN-algoritmi on yksi yksinkertaisimmista luokitusalgoritmeista. Tällainen yksinkertaisuus voi antaa erittäin kilpailukykyisiä tuloksia.NNN-algoritmia voidaan käyttää myös regressio-ongelmiin. Esitetystä metodologiasta lähimpien naapureiden keskiarvojen käyttäminen lähimpien naapureiden äänestämisen sijaan. KNN voidaan koodata yhdellä rivillä R: ssä. En ole vielä selvittänyt, miten voimme käyttää KNN-algoritmia SAS: ssa.

Pidin artikkelista hyödyllistä? Oletko käyttänyt muita koneoppimisen työkaluja viime aikoina? Aiotko käyttää KNN: ää missä tahansa liiketoimintaongelmassasi? Jos kyllä, kerro meille, miten aiot tehdä sen.

Jos pidät juuri lukemastasi & haluat jatkaa analytiikan oppimista, tilaa meidän sähköpostit, seuraa meitä twitterissä tai tykkää facebook-sivullamme.