Kuinka paine vaihtelee tilavuuden muutoksen aikana adiabaattisen paisumisen ja puristuksen aikana ihanteellisessa kaasussa? Tämä sivu on liite keskusteluun äänestä. Ilmanpaineessa oleva ilma on melkein ihanteellinen kaasu, ja äänen siirto ilmassa on lähellä adiabaattista normaalitaajuuksille ja siirtomäärille. (Palataan tähän olettamukseen jäljempänä.)
Ensimmäinen termodynamiikan laki liittää sisäisen energian dU muutoksen järjestelmän tekemään työhön dW ja siihen lisättyyn lämpö dQ: han.
dU = dQ – dW
Määritelmän mukaan lämmönvaihdin dQ = adiabaattisessa prosessissa 0. Tämän korvaaminen ensimmäisessä laissa ja järjestäminen antaa
0 = dQ = dU + dW
Toinen termi on helppoa: työ, joka on tehty dW, kun järjestelmä muuttaa tilavuuttaan V dV: llä, on PdV.
Ensimmäinen termi voi liittyä ominaislämpöön, joka määritellään lämpötilan muutosyksikköä kohti lisättynä lämpönä aineen moolia kohti. Jos lisätään lämpöä vakiotilavuudella, kaasu ei laajene eikä toimi. Joten lisätty lämpö lisää sisäistä energiaa U. Tästä seuraa, että määritelmän mukaan ominaislämpö vakiotilavuudella on 159f84ead0 ”>
, missä n on moolien lukumäärä. Siksi
Nyt ihanteellisen kaasun tilayhtälö on
nRT = PV ( ii)
missä R on kaasuvakio. Johdannaisten ottaminen antaa
Voimme nyt yhdistää yhtälöt (i) ja (iii) T: n poistamiseksi. (i) ja (ii) anna vastaavasti nämä lausekkeet ncv dT: lle:
PdV- ja VdP-termien kerääminen antaa
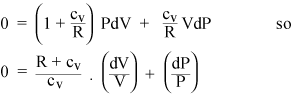
Jos kaasu on nyt ihanteellinen, sen sisäinen energia on kaikki kineettistä, joten sisäinen energia U riippuu vain T: stä. vakiopaineella tehty työ dW: se on vain PdV = nRdT. Joten, jos lisätään lämpöä kaasuun vakiopaineessa, meidän on lisälämpöä RdT jokaiselle kaasumoolille, sen lämmön lisäksi, joka meidän olisi lisättävä vakiotilavuudessa. Joten ihanteellisen kaasun ominaislämpö vakiopaineessa on vain cP = cv + R. Spesifisten lämmitysten suhteelle annetaan vakiosymboli:
. Joten meillä on
(iv)
Tämä on tärkein tulos, josta meidän on keskusteltava ääniaalloista: olemme juuri osoittaneet, että suhteellinen paineen muutos on – γ kertaa suhteellinen tilavuuden muutos tai γ kertaa tiheyden suhteellinen muutos.
Älkäämme kuitenkaan pysähtykö tässä, koska olemme vain muutaman rivin päässä tärkeästä tuloksesta. Tiedämme, että d (ln x) = dx / x (katso todiste laskelmasta). Joten voimme kirjoittaa edellinen yhtälö muodossa
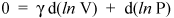
ja järjestä se uudelleen antamaan
(v)
Tästä syystä adiabaattinen prosessi ihanteellisessa kaasussa,
. (vi)
Pohdinnassa hyväksyt, että cP > cV: vakiotilavuus, kaikki th Laittamasi lämpö lisää sisäistä energiaa ja nostaa siten lämpötilaa. Jatkuvassa paineessa sinun ei tarvitse laittaa vain lämpöä, joka nostaa sisäistä energiaa, vaan myös lämmön määrä, joka on yhtä suuri kuin työ, joka tapahtuu järjestelmän lämpölaajenemisen yhteydessä. Ilman osalta y on noin 1,4.
Voimme tietysti nyt korvata tilan (ii) yhtälöstä kohdan (vi) nähdäksesi, kuinka P ja T tai T ja V liittyvät toisiinsa adiabaattisessa prosessissa.
Milloin ääni on adiabaattinen?
Mainitsimme edellä, että ”äänen lähetys ilmassa on lähellä adiabaattista normaalitaajuuksilla ja lähetysetäisyyksillä”. Milloin tämä epäonnistuu? Ääniaallon paine-maksimissa lämpötila on korkea. Joten odotamme, että jonkin verran lämpöä diffundoituu naapuripaineen minimiin. Tietysti puolessa aallon jaksossa lämmöllä ei ole paljon aikaa diffundoida puoli aallonpituutta. Kuitenkin lämmön hajaantumiseen kuluva aika kulkee etäisyyden neliönä. Joten tämä prosessi on vähemmän merkityksetön korkeille taajuuksille, koska lyhyempi puoli aallonpituus kompensoi enemmän kuin lyhyempi puolijakso. Tämä diffuusio ottaa mekaanisen energian pois aallosta, erityisesti korkeilla taajuuksilla, ja vaikutus lisääntyy siirtomatkan myötä.Tästä syystä (ja joskus myös muissa) etäiset äänet eivät ole vain vähemmän kovia, mutta myös vähemmän kirkkaita kuin läheiset.