by 0 comments on "5.3: Yksinkertaiset kaasulakit – Boylen laki, Charlesin laki ja Avogadron laki"

5.3: Yksinkertaiset kaasulakit – Boylen laki, Charlesin laki ja Avogadron laki


Paineen ja tilavuuden suhde: Boylen laki

Kun kaasuun kohdistuva paine kasvaa, kaasun tilavuus pienenee, koska kaasupartikkelit pakotetaan lähemmäksi toisiaan. Kääntäen, kun kaasun paine pienenee, kaasun tilavuus kasvaa, koska kaasupartikkelit voivat nyt liikkua kauemmas toisistaan. Sään ilmapallot kasvavat, kun ne nousevat ilmakehän läpi matalamman paineen alueille, koska kaasun tilavuus on kasvanut; eli ilmakehän kaasu aiheuttaa vähemmän painetta ilmapallon pinnalle, joten sisäkaasu laajenee, kunnes sisäinen ja ulkoinen paine ovat samat.

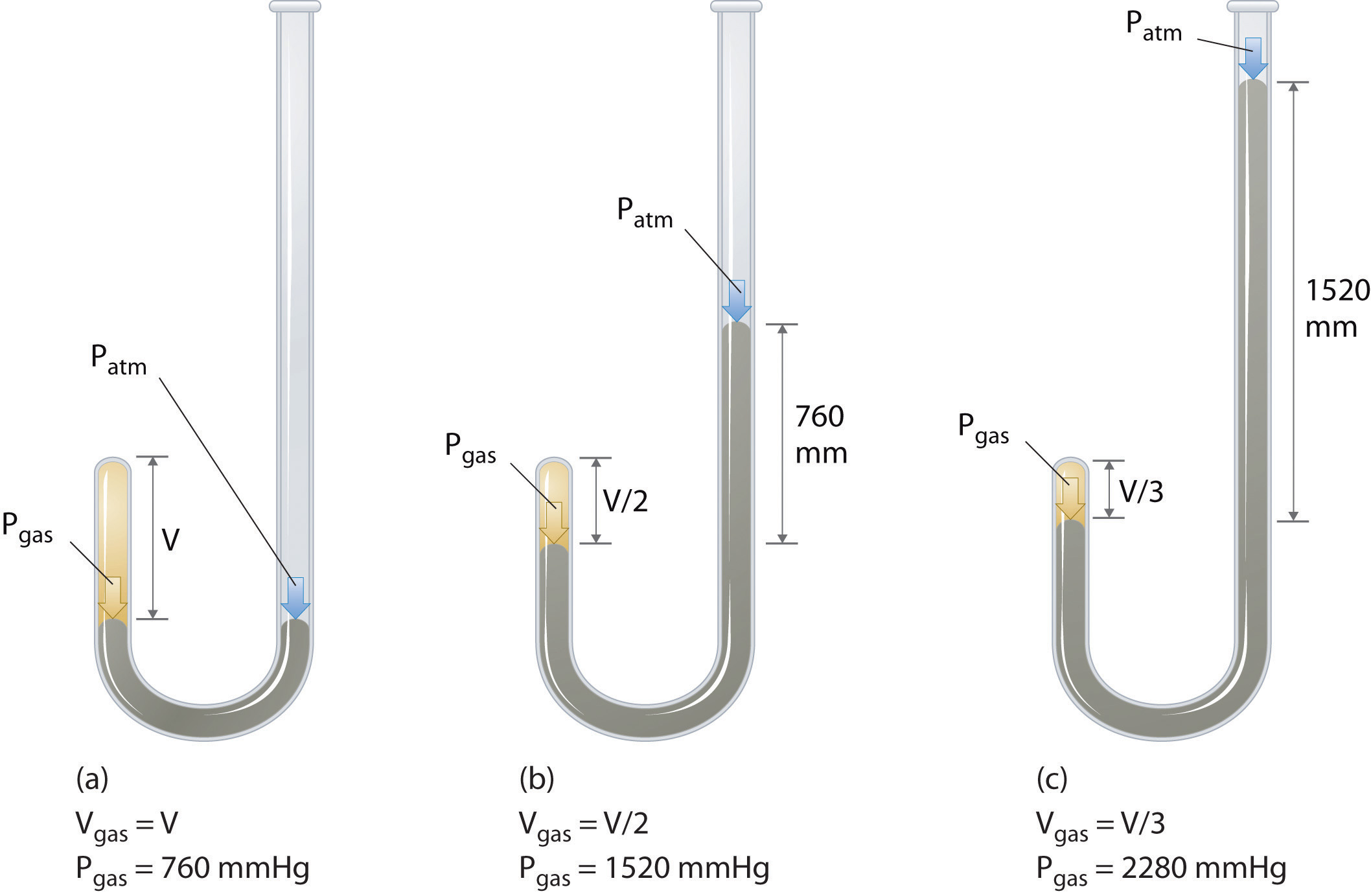
Kuva \ (\ PageIndex {1 } \): Boylen kokeilu J-muotoisen putken avulla kaasupaineen ja tilavuuden suhteen määrittämiseksi. (A) I tyypillisesti kaasu on paineessa 1 atm = 760 mmHg (elohopea on samalla korkeudella sekä näytteen sisältävässä varressa että ilmakehään avoimessa varressa); sen tilavuus on V. (b) Jos oikealle puolelle lisätään tarpeeksi elohopeaa, jotta kahden varren korkeusero olisi 760 mmHg, kaasun paine on 760 mmHg (ilmanpaine) + 760 mmHg = 1520 mmHg ja äänenvoimakkuus on V / 2. (c) Jos lisäksi 760 mmHg lisätään oikealla olevaan pylvääseen, kaasun kokonaispaine nousee 2280 mmHg: iin ja kaasun tilavuus laskee arvoon V / 3 (CC BY-SA-NC; pyynnöstä tuntematon) ).

Irlantilainen kemisti Robert Boyle (1627–1691) suoritti joitain varhaisimpia kokeita, joissa määritettiin paineen ja tilavuuden kvantitatiivinen suhde. kaasu. Boyle käytti J-muotoista putkea, joka oli osittain täytetty elohopealla, kuten kuvassa \ (\ PageIndex {1} \) esitetään. Näissä kokeissa pieni määrä kaasua tai ilmaa on loukussa elohopeapylvään yläpuolella ja sen tilavuus mitataan ilmakehän paineessa ja vakiolämpötilassa. Sitten kaadetaan lisää elohopeaa avoimeen varteen kaasunäytteen paineen lisäämiseksi. Kaasun paine on ilmakehän paine plus elohopeapylväiden korkeusero, ja tuloksena oleva tilavuus mitataan. Tätä prosessia toistetaan, kunnes joko avoimessa varressa ei ole enää tilaa tai kaasun tilavuus on liian pieni mitattavaksi tarkasti. Esimerkiksi Boylen omien kokeiden tiedot voidaan piirtää useilla tavoilla (kuva \ (\ PageIndex {2} \). Yksinkertainen käyrä \ (V \) vs. \ (P \) antaa käyrän, jota kutsutaan hyperbolaksi, ja paljastaa käänteisen suhteen paineen ja tilavuuden välillä: kun paine kaksinkertaistuu, tilavuus vähenee kaksi kertaa. Tämä suhde kahden suureen välillä kuvataan seuraavasti:

\

Molempien puolien jakaminen \ (P \) antaa yhtälön, joka kuvaa käänteistä suhdetta \ (P \) ja \ (V \):

\

tai

\

jossa symboli ∝ luetaan, on verrannollinen. ” Piirros V vs. 1 / P on siis suora viiva, jonka kaltevuus on yhtä suuri kuin yhtälöiden vakio yhtälöissä \ (\ ref {10.3.1} \) ja \ (\ ref {10.3.3} \). Yhtälö \ (\ ref {10.3.1} \) V: llä P: n sijasta antaa samanlaisen suhteen P: n ja 1 / V: n välillä. Vakion numeerinen arvo riippuu kokeessa käytetyn kaasun määrästä ja lämpötilasta, jossa Tämä paineen ja tilavuuden suhde tunnetaan Boylen lain mukaan sen löytäjän jälkeen, ja se voidaan todeta seuraavasti: Vakiolämpötilassa kiinteän määrän kaasun tilavuus on kääntäen verrannollinen sen paineeseen. laki käytännössä näkyy kuvassa \ (\ PageIndex {2} \).

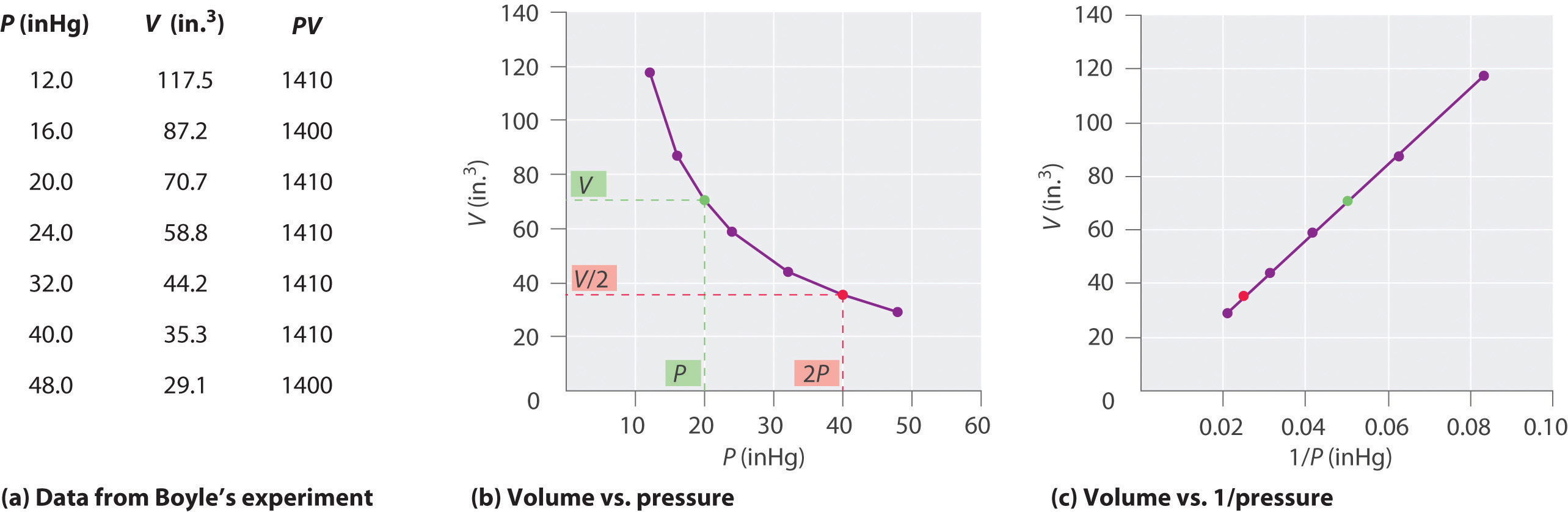
Kuva \ (\ PageIndex {2} \): Kaaviot Boylen tiedoista. (A) Tässä on todellisia tietoja tyypillisestä Boylen suorittamasta kokeesta. Boyle käytti ei-SI-yksiköitä tilavuuden (3 in cm eikä cm3) ja paineen mittaamiseen. (in. Hg eikä mmHg). (b) T hänen paineen ja tilavuuden juoni on hyperboli. Koska PV on vakio, paineen alentaminen kahdella kertoimella johtaa tilavuuden kaksinkertaiseen kasvuun ja päinvastoin. (c) Kaavio tilavuudesta vs. 1 / paine samoille tiedoille osoittaa käänteisen lineaarisen suhteen näiden kahden suureen välillä ilmaistuna yhtälöllä V = vakio / P (CC BY-SA-NC; pyynnöstä tuntematon).

Vakiolämpötilassa kiinteän kaasumäärän tilavuus on kääntäen verrannollinen sen paineeseen

Vastaa

Sähköpostiosoitettasi ei julkaista. Pakolliset kentät on merkitty *