Jäännösanalyysia suoritettaessa ”jäännökset vs. sopivat juoni” on yleisimmin luotu käyrä. Se on sirontakaavio jäännöksistä y-akselilla ja sovitetut arvot (arvioidut vasteet) x-akselilla. Kaaviota käytetään epälineaarisuuden, epätasaisten virheiden varianssien ja poikkeamien havaitsemiseen.
Katsotaanpa esimerkkiä nähdäkseen miltä ”hyvin käyttäytyvä” jäännöskaavio näyttää. Jotkut tutkijat (Urbano- Marquez et ai., 1989) olivat kiinnostuneita määrittämään, liittyykö alkoholin kulutus lineaarisesti lihasvoimaan vai eivät. Tutkijat mitasivat alkoholin (x) koko eliniän kulutuksen satunnaisotoksella n = 50 alkoholista miestä. deltalihaksen vahvuus (y) jokaisen henkilön ei-hallitsevassa käsivarressa. Saatujen tietojen sovitettu viivakaavio (alcoholarm.txt) näyttää tältä:
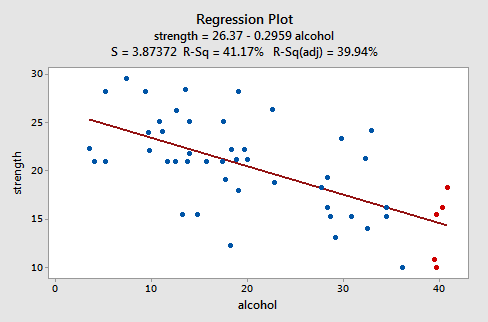
Juoni viittaa siihen, että alkoholin ja käsivoiman välillä on laskeva lineaarinen suhde. Se viittaa myös siihen, että tietojoukossa ei ole epätavallisia datapisteitä. Ja se havainnollistaa, että vaihtelu arvioidun regressioviivan ympärillä on vakio, mikä viittaa siihen, että oletus yhtäläisistä virheiden vaihteluista on kohtuullinen.
Tässä mitä vastaavat jäännökset vs. sovituskaavio näyttävät tietojoukolle ” yksinkertainen lineaarinen regressiomalli, jonka käsivarren vahvuus on vaste ja alkoholin kulutuksen taso ennustajana:
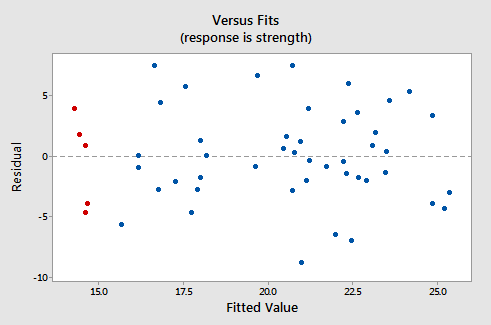
Huomaa, että määritelmän mukaisesti jäännökset näkyvät y-akselilla ja sovitetut arvot x-akselilla. Sinun pitäisi pystyä katsomaan taaksepäin datan sirontakaaviota ja nähdä, kuinka siellä olevat datapisteet vastaavat tässä jäljellä olevien ja vastaavien kuvaajien datapisteitä. Jos sinulla on vaikeuksia tehdä niin, katso alkuperäisen sirontakuvion viisi punaisena näkyvää datapistettä. Huomaa, että näiden miesten (joiden alkoholinkulutus on noin 40) ennustettu vaste (sovitettu arvo) on noin 14 . Huomaa myös kuvio, jossa viisi datapistettä poikkeavat arvioidusta regressioviivasta.
Katsokaa nyt, miten ja missä nämä viisi datapistettä esiintyvät jäännös- ja sovituskaaviossa. Niiden sovitettu arvo on noin 14 ja niiden poikkeama jäännös = 0-linjasta jakaa saman mallin kuin niiden poikkeama arvioidusta regressioviivasta. Näetkö yhteyden? Kaikilla datapisteillä, jotka putoavat suoraan arvioidulle regressioviivalle, on jäännös 0. Siksi jäännös = 0-rivi vastaa arvioitua regressioviivaa.
Tämä juoni on klassinen esimerkki hyvin käyttäytyvistä jäännös- ja sovituspiirteistä. Tässä ovat hyvin käyttäytyvän jäännös- ja sovituspiirroksen ominaisuudet ja mitä ne ehdottaa yksinkertaisten tarkoituksenmukaisuudesta Lineaarinen regressiomalli:
- Jäännökset ”pomppivat satunnaisesti” viivan 0 ympäri. Tämä viittaa siihen, että oletus, että suhde on lineaarinen, on kohtuullinen.
- Jäännökset muodostavat karkeasti ”vaakasuoran kaistan” 0-viivan ympärille. Tämä viittaa siihen, että virhetermien varianssit ovat samat.
- Kukaan jäännös ei ”erotu” jäännösten satunnaisesta perusmallista. Tämä viittaa siihen, että poikkeavuuksia ei ole.
Yleensä haluat, että jäännös- ja sovitustonttisi näyttävät jotain yllä olevalta juonelta. Älä unohda, että näiden juonien tulkinta on subjektiivista. Kokemukseni on ollut, että opiskelijat, jotka oppivat ensimmäistä kertaa jäännösanalyysin, tulkitsevat liikaa näitä juonia katsomalla jokaista kierrosta ja käännöstä mahdollisesti potentiaaliseksi ongelmaksi. Haluat erityisesti ole varovainen, kun painat liikaa jäännös- ja sovituspiirteisiin pienten tietojoukkojen perusteella. Joskus tietojoukot ovat aivan liian pieniä, jotta jäännösten ja sovituskuvien tulkinta olisi kannattavaa. Älä huoli! Opit – käytännön avulla – kuinka ”lukea” nämä juovat.