Oletetaan, että ilmaa pumpataan alas sileään pyöreään putkeen, jonka halkaisija on vakio lukuun ottamatta osaa keskellä, jossa putki kapenee puoleen halkaisijaan saakka, laajenee sitten uudelleen. Oletetaan, että kaikki halkaisijan muutokset tapahtuvat sujuvasti ja ilma virtaa tasaisesti putkea pitkin ilman pyörteitä tai pyörteitä.
Harjoittele
missä putkessa oletat paineen olevan suurin?
Vastaus
Useimmat ihmiset kysyivät tätä ensimmäistä kertaa ennustavat, että paine on suurin putken kapeassa osassa. Mutta itse asiassa, jos todella teemme kokeen, asettamalla painemittareita putken eri pisteisiin havaitsemme intuitiivisesti, että ilmanpaine on matalin siellä, missä ilma liikkuu nopeimmin!

Näemme miten tämä voisi olla, käytämme tekniikat, jotka kehitimme selvittämään, kuinka paine vaihteli kiinteässä nesteessä. Tapa, jolla teimme sen, muista, että piirtimme pienen nestesylinterin vapaan rungon kaavion. Koska tämä pieni sylinteri oli levossa, kokonaisvoima siihen oli nolla, joten nettopaine tasapainotti painoa. Harkitse nyt tasaisesti liikkuvaa nestettä. On hyödyllistä visualisoida virtaus piirtämällä virtaviivoja, viivoja siten, että niiden suunta on suunta, johon neste liikkuu kussakin kohdassa.

Nämä virtaviivat eivät todellakaan kerro vain, mihin suuntaan neste liikkuu, vaan antavat myös jonkinlaisen kuvan nopeudesta – missä ne tulevat lähemmäksi toisiaan, nesteen täytyy liikkua nopeammin, koska sama määrä nestettä virtaa kapeamman alueen läpi. Kuvittele nyt sylinteri ilmaa, joka liikkuu putkea pitkin, sen akseli yhdensuuntainen virtauksen kanssa. Ilmeisesti sen on nopeuduttava tullessaan putken kapeaan osaan – koska kapeaan osaan virtaa sama määrä ilmaa kuin leveä osa, sen on mentävä nopeammin.
Mutta jos pieni nestesylinteri kiihtyy, sitä on käytettävä voimalla, joka työntää sitä takaa.
Sen painolla ei ole merkitystä tässä, koska se liikkuu vaakasuunnassa. Siksi ainoa siihen vaikuttava voima on paine, ja meidän on pääteltävä, että sen takana oleva paine on suurempi kuin sen edessä oleva paine. Siksi paineen on laskettava kapeaan osaan tultaessa. Selvittääkseen, mitä tapahtuu, piirrämme melko suuren sylinterin:
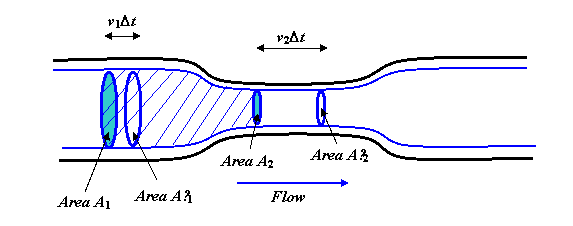
Neste virtaa tasaisesti ja sujuvasti pitkin putki. Paksut siniset viivat ovat suoraviivaisia, itse asiassa sinun pitäisi kuvitella kiertävän koko kaaviota keskiakselin ympäri kolmiulotteisen kuvan saamiseksi, ja sinisistä viivoista tulisi sylinteri, kapeammalla ”kaulan” osalla, joka toistaa
Tarkastellaan nyt nestekerros esitettyjen suoraviivojen sisällä ja suljettu molemmista päistä pyöreillä alueilla A1 ja A2. Nesteen virtausnopeuden A1 läpi on oltava sama kuin nesteen virtausnopeuden. virtaus A2: n poikki, koska tasaisessa virtauksessa neste ei voi kerääntyä keskelle (tai tyhjentyä myöskään sieltä). A1: n läpi yhdessä sekunnissa virtaava tilavuus on v1A1. (Kuvitellaksesi tämän, kuvittele pitkä suora putki ilman kapeaa Jos neste virtaa nopeudella, esimerkiksi 3 metriä sekunnissa, niin sekunnissa kaikki neste, joka oli 3 metrin säteellä ylävirran puolella olevasta alueesta A1, on valunut läpi.)
Joten, virtaus A1: n yli on yhtä suuri kuin virtaus A2: n yli, \
(alaviite: Ehkä on syytä mainita, että oletamme implisiittisesti nopeuden ty on sama kaikissa alueen A1 pisteissä. Kaikilla todellisilla nesteillä on jonkin verran viskositeettia (kitkaa) ja ne liikkuvat hitaammin putken sivujen lähellä kuin keskellä. Keskustelemme tästä myöhemmin. Toistaiseksi pidämme ”ihanteellisena” nesteenä termiä, jota käytetään silloin, kun viskositeetti jätetään huomiotta. Itse asiassa tulos on ok – olisimme voineet ottaa pienen alueen A1 kaukana sivuilta, jotta nopeus olisi ollut sama koko alueelle, mutta se olisi antanut paljon vähemmän selkeän kaavion.)
Olemme nyt valmiita tutkimaan nesteen kineettisen energian kasvua, kun se kiihtyy kapeaan osaan, ja ymmärrä, kuinka paine-ero teki sen nopeuttamiseksi tarvittavan työn.
\
Ainoa mahdollinen lähde tälle energian lisäykselle on paineen tekemä työ nesteen työntämiseksi sisään kapea osa.
\
Joten tämä on työtä, joka on tehty nestepalassamme työntämällä nestettä takaa – mutta se ei ole tarinan loppu, koska palanen neste itse toimii työntämällä nestettä sen eteen, joten löytääksemme palan energian kokonaiskasvun, meidän on vähennettävä sen tekemä ulkoinen työ.Toisin sanoen nesteemme kohdistuvalla paineella tehtyjen töiden kokonaismäärä on
\
muistaa että \ (A_1v_1 = A_2v_2 \).
Tämän tekemän työn on oltava yhtä suuri kineettisen energian muutos, joten
\
josta
\
Tämä on Bernoullin yhtälö.
\.
Avustajat ja attribuutit
- Michael Fowler (Beams-professori, fysiikan laitos, Virginian yliopisto)