Come varia la pressione al variare del volume durante lespansione e la compressione adiabatiche in un gas ideale? Questa pagina è unappendice alla nostra discussione sul suono. Laria a pressione atmosferica è un gas quasi ideale e la trasmissione del suono nellaria è vicina alladiabatica per le frequenze e le distanze di trasmissione normali. (Ritorniamo a questo assunto di seguito.)
La prima legge della termodinamica mette in relazione la variazione dellenergia interna dU con il lavoro dW svolto da un sistema e il calore dQ aggiunto ad esso.
dU = dQ – dW
Per definizione, in un processo adiabatico, il calore scambiato dQ = 0. Sostituendo questo nella prima legge e riorganizzando si ottiene
0 = dQ = dU + dW
Il secondo termine è facile: il lavoro svolto dW quando un sistema cambia il suo volume V di dV è PdV.
Il primo termine può essere correlato al calore specifico, che è definito come il calore aggiunto per unità di variazione di temperatura per mole di sostanza. Se aggiungiamo calore a volume costante, il gas non si espande e quindi non “funziona. Quindi il calore aggiunto aumenta lenergia interna U. Quindi segue quella definizione che il calore specifico a volume costante è ![]() , dove n è il numero di moli. Quindi
, dove n è il numero di moli. Quindi
Ora lequazione di stato di un gas ideale è
nRT = PV ( ii)
dove R è la costante dei gas. Prendendo le derivate si ottiene
Ora possiamo combinare le equazioni (i) e (iii) per eliminare T. (i) e (ii) fornire rispettivamente queste espressioni per ncv dT:
La raccolta dei termini PdV e VdP fornisce
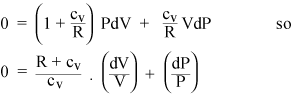
Ora se il gas è ideale, la sua energia interna è tutta cinetica, quindi lenergia interna U dipende solo da T. Dallequazione di stato di un gas ideale (ii), possiamo calcolare il lavoro dW svolto a pressione costante: è solo PdV = nRdT. Quindi, se aggiungiamo calore a un gas a pressione costante, dobbiamo riscaldare ulteriormente RdT per ogni mole di gas, oltre al calore che dovremmo aggiungere a volume costante. Quindi il calore specifico di un gas ideale a pressione costante è solo cP = cv + R. Al rapporto dei calori specifici viene assegnato un simbolo standard:
. Quindi abbiamo
(iv)
Questo è il risultato principale di cui abbiamo bisogno per discutere le onde sonore: abbiamo appena dimostrato che la variazione proporzionale della pressione è – γ volte la variazione proporzionale del volume o γ volte la variazione proporzionale della densità.
Non fermiamoci qui, tuttavia, perché siamo solo a poche righe di distanza da un risultato importante. Sappiamo che d (ln x) = dx / x (vedi calcolo per una dimostrazione). Quindi possiamo scrivere lequazione precedente come
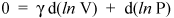
e riorganizzalo per fornire
(v)
Quindi, per un processo adiabatico in un gas ideale,
. (vi)
Riflettendoci, accetterete che cP > cV: At volume costante, tutto th Il calore che immetti va ad aumentare lenergia interna e quindi ad aumentare la temperatura. A pressione costante, è necessario immettere non solo il calore che innalza lenergia interna, ma anche una quantità di calore pari al lavoro svolto quando il sistema subisce la dilatazione termica. Per laria, γ è circa 1,4.
Naturalmente, ora possiamo sostituire in (vi) dallequazione di stato (ii) per vedere come P e T o T e V sono correlati per un processo adiabatico.
Quando il suono è adiabatico?
Abbiamo già detto che “la trasmissione del suono nellaria è vicina alladiabatica per frequenze e distanze di trasmissione normali”. Quando fallisce? Alla pressione massima in unonda sonora, la temperatura è alta. Quindi ci aspettiamo che un po di calore si diffonda ai minimi di pressione vicini. Ovviamente in mezzo periodo di unonda sonora, non cè molto tempo perché il calore diffonda una mezza lunghezza donda. Tuttavia, il tempo impiegato per la diffusione del calore è pari al quadrato della distanza. Quindi questo processo è meno trascurabile per le alte frequenze, perché la metà lunghezza donda più corta compensa maggiormente il semiperiodo più corto. Questa diffusione sottrae energia meccanica allonda, soprattutto alle alte frequenze, e leffetto aumenta con la distanza di trasmissione.Per questo motivo (e talvolta per altri), i suoni distanti non solo sono meno forti, ma anche meno luminosi di quelli vicini.