A suma es el resultado de una suma. Por ejemplo, al sumar 1, 2, 3 y 4 se obtiene la suma 10, escrita
 |
(1)
|
Los números que se suman se denominan sumandos o, a veces, sumandos. La operación de suma también se puede indicar usando una sigma mayúscula con los límites superior e inferior escritos arriba y abajo, y el índice indicado abajo. Por ejemplo, la suma anterior podría escribirse
 |
(2)
|
El La suma de una lista de números se implementa como Total.
Una suma
 |
(3)
|
en el que cada término 
viene dado por alguna regla fija (es decir, 
es un pozo -definida) se llama serie (finita), y si el número de términos 
es infinito, la suma se llama serie infinita (o, a menudo, simplemente «serie»). Una suma de la forma
 |
(4)
|
se llama serie geométrica .
Las condiciones para la convergencia de una serie se pueden determinar en Wolfram Language usando SumConvergence.
La suma de potencia finita general
 |
(5)
|
puede ser dado por la expresión
 |
(6)
|
que es equivalente a la fórmula de Faulhaber, donde la notación 
significa la cantidad en la pregunta se eleva a la potencia adecuada 
y todos los términos de la forma 
se reemplazan por los correspondientes Números de Bernoulli 
.
Una identidad divertida debida a J. Ziegenbein (com. Pers. comm., 19 de junio de 2002) se deriva de la identidad
 |
(7)
|
que se puede escribir
 |
(8)
|
Por lo tanto, 
, por ejemplo, se puede escribir en las formas equivalentes
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
y así sucesivamente.
El teorema de Nicomachus da una curiosa expresión para la suma de potencias 
.
Las sumas especiales incluyen
 |
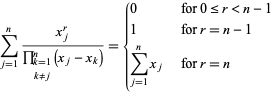(13)
|
y
 |
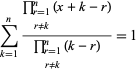(14)
|
Para minimizar la suma de un conjunto de cuadrados de números 
sobre un número determinado 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
tome la derivada.
 |
(17)
|
Al resolver 
se obtiene
 |
(18)
|
por lo que 
se minimiza cuando 
se establece en significar.