¿Cómo varía la presión con el cambio de volumen durante la expansión y compresión adiabática en un gas ideal? Esta página es un apéndice de nuestra discusión sobre el sonido. El aire a presión atmosférica es un gas casi ideal y la transmisión de sonido en el aire es casi adiabática para frecuencias y distancias de transmisión normales. (Volvemos a esta suposición a continuación).
La primera ley de la termodinámica relaciona el cambio en la energía interna dU con el trabajo dW realizado por un sistema y el calor dQ que se le agrega.
dU = dQ – dW
Por definición, en un proceso adiabático, el calor intercambiado dQ = 0. Sustituyendo esto en la primera ley y reordenando da
0 = dQ = dU + dW
El segundo término es fácil: el trabajo realizado dW cuando un sistema cambia su volumen V por dV es PdV.
El primer término puede estar relacionado con el calor específico, que se define como el calor agregado por unidad de cambio de temperatura por mol de sustancia. Si agregamos calor a volumen constante, entonces el gas no se expande y, por lo tanto, no funciona. Por lo tanto, el calor agregado aumenta la energía interna U. Por lo tanto, la definición de que el calor específico a volumen constante es ![]() , donde n es el número de moles. Por lo tanto
, donde n es el número de moles. Por lo tanto
Ahora la ecuación de estado de un gas ideal es
nRT = PV ( ii)
donde R es la constante del gas. Tomando derivadas da
Ahora podemos combinar las ecuaciones (i) y (iii) para eliminar T. (i) y (ii) dar respectivamente estas expresiones para ncv dT:
La recopilación de los términos de PdV y VdP da
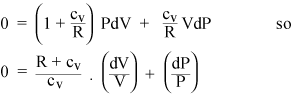
Ahora bien, si el gas es ideal, su energía interna es toda cinética, por lo que la energía interna U depende solo de T. A partir de la ecuación de estado de un gas ideal (ii), podemos calcular el trabajo dW realizado a presión constante: es solo PdV = nRdT. Entonces, si agregamos calor a un gas a presión constante, tenemos que calentar más RdT por cada mol de gas, más allá del calor que deberíamos tener que agregar a volumen constante. Por tanto, el calor específico de un gas ideal a presión constante es simplemente cP = cv + R. La relación de los calores específicos recibe un símbolo estándar:
. Entonces tenemos
(iv)
Este es el resultado principal que necesitamos para discutir las ondas sonoras: acabamos de demostrar que el cambio proporcional en la presión es – γ veces el cambio proporcional en el volumen o γ veces el cambio proporcional en la densidad.
Sin embargo, no nos detengamos aquí, porque estamos a solo unas líneas de un resultado importante. Sabemos que d (ln x) = dx / x (ver cálculo para una prueba). Entonces podemos escribir la ecuación anterior como
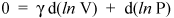
y reordenarlo para dar
(v)
Por lo tanto, para un proceso adiabático en un gas ideal,
. (vi)
Pensándolo bien, «estará de acuerdo en que cP > cV: En volumen constante, todo el El calor que pones sirve para aumentar la energía interna y así elevar la temperatura. A presión constante, es necesario introducir no solo el calor que eleva la energía interna, sino también una cantidad de calor igual al trabajo realizado cuando el sistema sufre una expansión térmica. Para el aire, γ es aproximadamente 1,4.
Por supuesto, ahora podemos sustituir en (vi) de la ecuación del estado (ii) para ver cómo se relacionan P y T o T y V para un proceso adiabático.
¿Cuándo es adiabático el sonido?
Mencionamos anteriormente que «la transmisión de sonido en el aire es cercana a la adiabática para frecuencias y distancias de transmisión normales». ¿Cuándo falla esto? A la presión máxima en una onda de sonido, la temperatura es alta. Por lo tanto, esperamos que algo de calor se difunda a los mínimos de presión vecinos. Por supuesto, en medio período de una onda de sonido, no hay mucho tiempo para que el calor difunda la mitad de la longitud de onda. Sin embargo, el tiempo necesario para que el calor se difunda se expresa como el cuadrado de la distancia. Por tanto, este proceso es menos despreciable para las frecuencias altas, porque la mitad de longitud de onda más corta compensa con creces la mitad del período más corto. Esta difusión extrae energía mecánica de la onda, especialmente a altas frecuencias, y el efecto aumenta con la distancia de transmisión.Por esta razón (y a veces otras), los sonidos distantes no solo son menos fuertes, sino también menos brillantes que los cercanos.