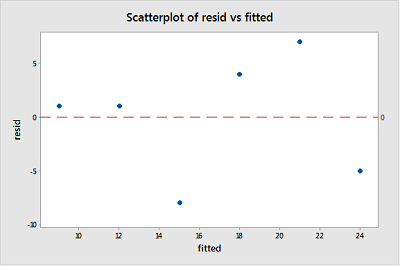
Cuando se realiza un análisis de residuos, un «gráfico de residuos frente a ajustes» es el gráfico creado con más frecuencia. Es un diagrama de dispersión de residuos en el eje y y valores ajustados (respuestas estimadas) en el eje x. La gráfica se usa para detectar no linealidad, variaciones de error desiguales y valores atípicos.
Veamos un ejemplo para ver cómo se ve una gráfica residual «bien comportada». Algunos investigadores (Urbano- Márquez, et al., 1989) estaban interesados en determinar si el consumo de alcohol estaba o no relacionado linealmente con la fuerza muscular. Los investigadores midieron el consumo total de alcohol durante toda la vida (x) en una muestra aleatoria de n = 50 hombres alcohólicos. También midieron la fuerza (y) del músculo deltoides en el brazo no dominante de cada persona. Una gráfica de línea ajustada de los datos resultantes, (alcoholarm.txt), se ve así:
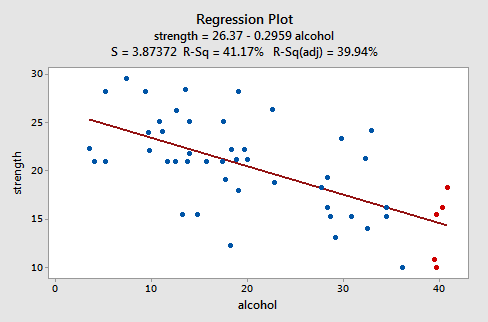
La gráfica sugiere que existe una relación lineal decreciente entre el alcohol y la fuerza del brazo. También sugiere que no hay puntos de datos inusuales en el conjunto de datos. Además, ilustra que la variación alrededor de la línea de regresión estimada es constante, lo que sugiere que la suposición de varianzas de error iguales es razonable.
A continuación, se muestra cómo se ve la gráfica de residuales versus ajustes correspondientes para el conjunto de datos. modelo de regresión lineal simple con la fuerza del brazo como respuesta y el nivel de consumo de alcohol como predictor:
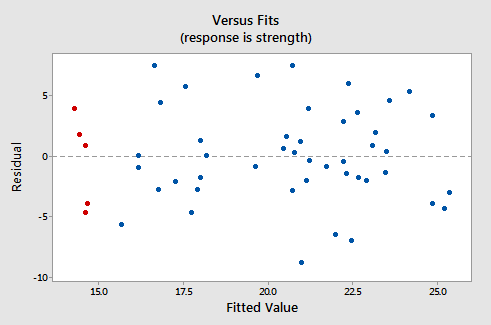
Tenga en cuenta que, como se define, los residuales aparecen en el eje y y los valores ajustados aparecen en el eje x. Debería poder mirar hacia atrás en el gráfico de dispersión de los datos y ver cómo los puntos de datos allí se corresponden con los puntos de datos en el gráfico de ajustes versus residuales aquí. En caso de que tenga problemas para hacer eso, observe los cinco puntos de datos en el gráfico de dispersión original que aparecen en rojo. Tenga en cuenta que la respuesta prevista (valor ajustado) de estos hombres (cuyo consumo de alcohol es de alrededor de 40) es aproximadamente 14 . Además, observe el patrón en el que los cinco puntos de datos se desvían de la línea de regresión estimada.
Ahora observe cómo y dónde aparecen estos cinco puntos de datos en la gráfica de residuos versus ajustes. Su valor ajustado es aproximadamente 14 y su desviación de la línea residual = 0 comparte el mismo patrón que su desviación de la línea de regresión estimada. ¿Ves la conexión? Cualquier punto de datos que caiga directamente en la línea de regresión estimada tiene un residual de 0. Por lo tanto, el residual = La línea 0 corresponde a la línea de regresión estimada.
Esta gráfica es un ejemplo clásico de una gráfica de residuos versus ajustes con buen comportamiento. Estas son las características de una gráfica de residuos versus ajustes con buen comportamiento y lo que Sugerir sobre la idoneidad de la simpl El modelo de regresión lineal:
- Los residuos «rebotan aleatoriamente» alrededor de la línea 0. Esto sugiere que la suposición de que la relación es lineal es razonable.
- Los residuos forman aproximadamente una «banda horizontal» alrededor de la línea 0. Esto sugiere que las varianzas de los términos de error son iguales.
- Ningún residuo «se destaca» del patrón aleatorio básico de residuos. Esto sugiere que no hay valores atípicos.
En general, desea que los gráficos de residuales vs. ajustes se parezcan al gráfico anterior. No olvide, sin embargo, que interpretar estas tramas es subjetivo. Mi experiencia ha sido que los estudiantes que aprenden el análisis residual por primera vez tienden a sobreinterpretar estas tramas, y consideran cada giro y giro como algo potencialmente problemático. tenga cuidado de no poner demasiado peso en las gráficas de residuales vs. ajustes basadas en pequeños conjuntos de datos. A veces, los conjuntos de datos son demasiado pequeños para hacer que valga la pena interpretar una gráfica de residuos frente a ajustes. ¡No se preocupe! Aprenderá, con la práctica, cómo «leer» estos gráficos.