Suponga que se bombea aire por un tubo redondo liso, que tiene un diámetro constante excepto por una sección en el medio donde el tubo se estrecha hasta la mitad del diámetro, luego se ensancha nuevamente. Suponga que todos los cambios de diámetro se producen sin problemas y que el aire fluye de manera constante por el tubo, sin remolinos ni turbulencias.
Ejercicio
¿En qué parte del tubo espera que lo haga? ¿La presión será mayor?
Respuesta
La mayoría de las personas que preguntaron esto por primera vez predicen que la presión será mayor en la parte estrecha del tubo. Pero de hecho, si realmente hacemos el experimento, colocando manómetros en varios puntos a lo largo del tubo, encontraremos, contrariamente a la intuición, que la presión del aire es más baja donde el aire se mueve más rápido.

Para ver cómo podría ser esto, aplicaremos las técnicas que desarrollamos para encontrar cómo variaba la presión en un fluido estacionario. Recuerde que la forma en que lo hicimos fue dibujando un diagrama de cuerpo libre para un pequeño cilindro de fluido. Dado que este pequeño cilindro estaba en reposo, la fuerza total sobre él era cero, por lo que la presión neta equilibraba el peso. Ahora considere un fluido en constante movimiento. Es útil visualizar el flujo dibujando líneas de corriente, líneas tales que su dirección sea la dirección en la que se mueve el fluido en cada punto.

En realidad, estas líneas de corriente no solo le indican la dirección en la que se mueve el fluido, sino que también le dan una idea de la velocidad: cuando se acercan, el fluido debe moverse más rápido, porque fluye la misma cantidad de fluido a través de una región más estrecha. Imagine ahora un cilindro de aire moviéndose a lo largo de la tubería, su eje paralelo a la línea de corriente. Obviamente, debe acelerarse a medida que ingresa a la parte estrecha del tubo; dado que la misma cantidad de aire fluye a través de la parte estrecha que de la parte ancha, debe ir más rápido.
Pero si la pequeña cilindro de fluido está acelerando, debe ser accionado por una fuerza que lo empuje desde atrás.
Su peso es irrelevante aquí, ya que se mueve horizontalmente. Por lo tanto, la única fuerza que actúa sobre él es la presión, y tenemos que concluir que la presión en su espalda es mayor que la presión en su frente. Por lo tanto, la presión debe descender al entrar en la parte estrecha. Para aclarar más lo que está sucediendo, dibujaremos un cilindro bastante grande:
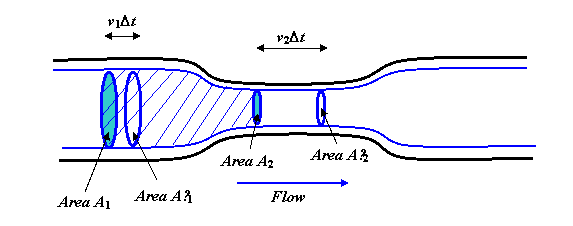
El fluido fluye de manera constante y suave el tubo. Las gruesas líneas azules son líneas aerodinámicas; de hecho, debería imaginarse rotando todo el diagrama alrededor del eje central para obtener una imagen tridimensional, y las líneas azules se convertirían en un cilindro, con una sección de «cuello» más estrecha, haciendo eco de la forma del
Ahora considere el cuerpo de fluido dentro de las líneas de corriente que se muestran, y cubierto en los dos extremos por las áreas circulares A1 y A2. La tasa de flujo de fluido a través de A1 debe ser la misma que la tasa de flujo a través de A2, porque en flujo constante el fluido no puede acumularse en el medio (o agotarse desde allí tampoco). El volumen que fluye a través de A1 en un segundo es v1A1. (Para ver esto, imagine una tubería larga y recta sin un estrecho Si el fluido fluye a, digamos, 3 metros por segundo, entonces en un segundo todo el fluido que estaba dentro de los 3 metros del área A1 en el lado de aguas arriba habrá pasado.)
Entonces, el flujo a través de A1 es igual al flujo a través de A2, \
(Nota a pie de página: tal vez valga la pena mencionar que estamos asumiendo implícitamente la velocidad ty es el mismo en todos los puntos del área A1. Cualquier fluido real tiene cierta viscosidad (fricción) y se moverá más lentamente cerca de los lados de la tubería que en el medio. Hablaremos de esto más tarde. Por ahora, consideramos un fluido «ideal», el término que se usa cuando se ignora la viscosidad. De hecho, el resultado que obtenemos es correcto: podríamos haber tomado un área pequeña A1 lejos de los lados, por lo que la velocidad habría sido lo mismo para toda el área, pero eso habría dado un diagrama mucho menos claro.)
Ahora estamos listos para examinar el aumento en la energía cinética del fluido a medida que se acelera hacia la parte estrecha, y comprender cómo la diferencia de presión hizo el trabajo necesario para acelerarla.
\
La única fuente posible para este aumento de energía es el trabajo realizado por la presión para empujar el fluido hacia la parte estrecha.
\
Así que este es el trabajo realizado en nuestro trozo de fluido por el fluido que lo empuja desde atrás, pero ese no es el final de la historia, porque nuestro trozo de el fluido en sí funciona empujando el fluido frente a él, por lo que para encontrar el aumento total en la energía de nuestro trozo, debemos restar el trabajo externo que realiza.Es decir, el trabajo total realizado por la presión sobre nuestro fluido es
\
recordando que \ (A_1v_1 = A_2v_2 \).
Este trabajo realizado debe ser igual el cambio en la energía cinética, entonces
\
de la cual
\
Esta es la ecuación de Bernoulli.
\.
Contribuyentes y Atribuciones
- Michael Fowler (Profesor de Beams, Departamento de Física, Universidad de Virginia)