A. Summe ist das Ergebnis einer Addition. Zum Beispiel ergibt das Addieren von 1, 2, 3 und 4 die Summe 10, geschrieben
 |
(1)
|
Die summierten Zahlen werden als Addenden oder manchmal als Summanden bezeichnet. Die Summierungsoperation kann auch unter Verwendung eines Kapitalsigmas mit Ober- und Untergrenzen oben und unten und dem unten angegebenen Index angegeben werden. Zum Beispiel könnte die obige Summe geschrieben werden:
 |
(2)
|
Die Die Summe einer Liste von Zahlen wird als Summe implementiert.
Eine Summe
 |
(3)
|
, in dem jeder Begriff 
durch eine feste Regel gegeben ist (dh 
ist ein Brunnen -definierte Folge) wird als (endliche) Reihe bezeichnet, und wenn die Anzahl der Terme 
unendlich ist, wird die Summe als unendliche Reihe (oder oft nur als „Reihe“) bezeichnet. Eine Summe der Form
 |
(4)
|
wird als geometrische Reihe bezeichnet
Die Bedingungen für die Konvergenz einer Reihe können in der Wolfram-Sprache mithilfe von SumConvergence bestimmt werden.
Die allgemeine endliche Potenzsumme
 |
(5)
|
kann durch den Ausdruck
 |
(6)
|
entspricht der Formel von Faulhaber, wobei die Notation 
die Menge in bedeutet Die Frage wird an die entsprechende Stelle 
gestellt, und alle Begriffe der Form 
werden durch die entsprechenden ersetzt Bernoulli-Nummern 
.
Eine amüsante Identität aufgrund von J. Ziegenbein (pers. comm., 19. Juni 2002) folgt aus der Identität
 |
(7)
|
was geschrieben werden kann
 |
(8)
|
Daher 
kann beispielsweise in den entsprechenden Formen geschrieben werden
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
und so weiter.
Der Satz von Nicomachus gibt einen merkwürdigen Ausdruck für die Potenzsumme 
.
Spezielle Summen umfassen
 |
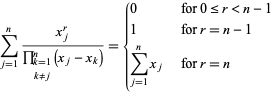(13)
|
und
 |
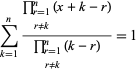(14)
|
Zum Minimieren der Summe einer Menge von Quadraten Anzahl 
über eine bestimmte Zahl 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
nehmen Sie die Ableitung.
 |
(17)
|
Wenn Sie nach 
suchen, erhalten Sie
 |
(18)
|
so wird 
minimiert, wenn 
auf gesetzt ist meine.