Steigung
Zusätzlich zu seiner bekannten Bedeutung hat das Wort „Steigung“ eine genaue mathematische Bedeutung. Die Steigung einer Linie ist der Anstieg über den Lauf oder die Änderung von y geteilt durch die Änderung von x. Um die Steigung einer Linie zu ermitteln, wählen Sie zwei beliebige Punkte auf der Linie aus. Subtrahieren Sie dann ihre x-Koordinaten und subtrahieren Sie ihre y-Koordinaten in derselben Reihenfolge. Teilen Sie die Differenz der y-Koordinaten durch die Differenz der x-Koordinaten:
Bei zwei Punkten (x1, y1) und (x2, y2) Auf einer Linie ist die Steigung der Linie gleich:
m = =
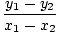
Negative Steigung
Wenn eine Linie eine positive Steigung aufweist (dh m > 0), dann nimmt y immer zu, wenn x zunimmt, und y nimmt immer ab, wenn x abnimmt. Der Graph der Linie beginnt also unten links und geht nach rechts oben.
Oft ist die Steigung einer Linie jedoch negativ. Eine negative Steigung bedeutet, dass y immer abnimmt, wenn x zunimmt, und y immer zunimmt, wenn x abnimmt. Hier ist ein Beispiel für ein Diagramm mit negativer Steigung:
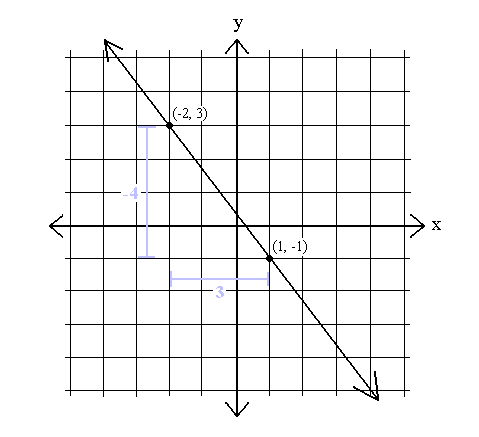
m =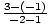 
= 
= – 
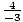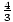
Wenn also x um 3 zunimmt, nimmt y um 4 ab und wenn x um 3 abnimmt, nimmt y um 4 zu.
Horizontale und vertikale Linien
Manchmal Wir werden Gleichungen sehen, deren Graphen horizontale Linien sind. Dies sind Diagramme, in denen y konstant bleibt, dh in denen y1 – y2 = 0 für zwei beliebige Punkte auf der Linie ist:
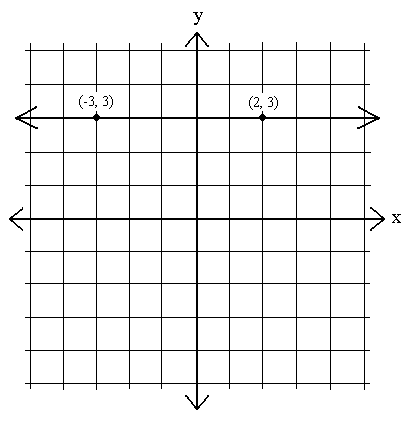
m =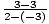 
= 
= 0.
Die Steigung einer horizontalen Linie ist 0. Mit anderen Worten, wenn x zunimmt oder abnimmt, ändert sich y nicht. x nimmt jeden möglichen Wert bei einem bestimmten y-Wert an.
Wir werden auch Gleichungen sehen, deren Graphen vertikale Linien sind. Dies sind Diagramme, in denen x konstant bleibt, dh in denen x1 – x2 = 0 für zwei beliebige Punkte auf der Linie ist:
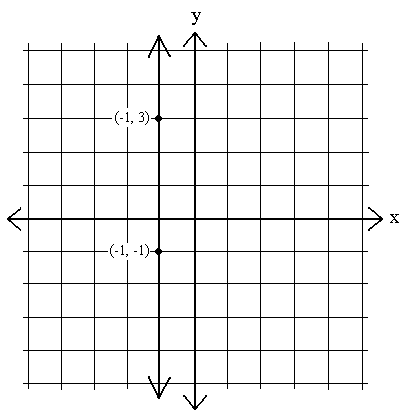
m =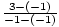 
= 
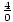= undefiniert. Wir können eine Zahl nicht durch Null teilen.
Die Steigung einer vertikalen Linie ist undefiniert. X nimmt nicht zu oder ab. Vielmehr nimmt y jeden möglichen Wert bei einem bestimmten x-Wert an.