Einführung in k-Nearest Neighbors: Ein leistungsstarker Algorithmus für maschinelles Lernen (mit Implementierung in Python & R)

Hinweis: Dieser Artikel wurde ursprünglich am 10. Oktober 2014 veröffentlicht und am aktualisiert 27. März 2018

Übersicht

• Verstehen Sie den nächsten Nachbarn (KNN) – einen der beliebtesten Algorithmen für maschinelles Lernen
• Lernen Sie die Arbeitsweise von kNN in Python
• Wählen Sie einfach den richtigen Wert von k

Einführung

In den vier Jahren In meiner Karriere als Data Science habe ich mehr als 80% Klassifizierungsmodelle und nur 15-20% Regressionsmodelle erstellt. Diese Verhältnisse können branchenweit mehr oder weniger verallgemeinert werden. Der Grund für diese Tendenz zu Klassifizierungsmodellen liegt darin, dass die meisten analytischen Probleme darin bestehen, eine Entscheidung zu treffen.

Wird beispielsweise ein Kunde abreiben oder nicht, sollten wir Kunden X ansprechen Digitale Kampagnen, unabhängig davon, ob der Kunde ein hohes Potenzial hat oder nicht usw. Diese Analysen sind aufschlussreicher und direkt mit einer Implementierungs-Roadmap verknüpft.

In diesem Artikel werden wir über eine andere weit verbreitete Klassifikationstechnik für maschinelles Lernen sprechen, die als K-Nearest Neighbours (KNN) bezeichnet wird. Unser Fokus wird in erster Linie darauf liegen, wie der Algorithmus funktioniert und wie sich der Eingabeparameter auf die Ausgabe / Vorhersage auswirkt.

Hinweis: Personen, die lieber durch Videos lernen möchten, können dies auch in unserem kostenlosen Kurs lernen – K- Nearest Neighbors (KNN) -Algorithmus in Python und R. Wenn Sie ein absoluter Anfänger in Data Science und maschinellem Lernen sind, lesen Sie unser Certified BlackBelt-Programm –

• Certified AI & ML Blackbelt + Programm

Inhaltsverzeichnis

• Wann verwenden wir den KNN-Algorithmus?
• Wie funktioniert das? KNN-Algorithmus funktioniert?
• Wie wählen wir den Faktor K aus?
• Aufschlüsselung – Pseudocode von KNN
• Implementierung in Python von Grund auf
• Vergleich unseres Modells mit scikit-learn

Wann verwenden wir den KNN-Algorithmus?

KNN kann für beide verwendet werden Vorhersageprobleme bei Klassifizierung und Regression. Es wird jedoch häufiger bei Klassifizierungsproblemen in der Industrie verwendet. Um eine Technik zu bewerten, betrachten wir im Allgemeinen drei wichtige Aspekte:

1. Einfache Interpretation der Ausgabe

2. Berechnungszeit

3. Vorhersagekraft

Nehmen wir einige Beispiele, um KNN in der Skala zu platzieren:

Der KNN-Algorithmus berücksichtigt alle Parameter von Überlegungen. Es wird häufig wegen seiner einfachen Interpretation und geringen Berechnungszeit verwendet.

Wie funktioniert der KNN-Algorithmus?

Nehmen wir einen einfachen Fall Verstehe diesen Algorithmus. Es folgt eine Verteilung von roten Kreisen (RC) und grünen Quadraten (GS):

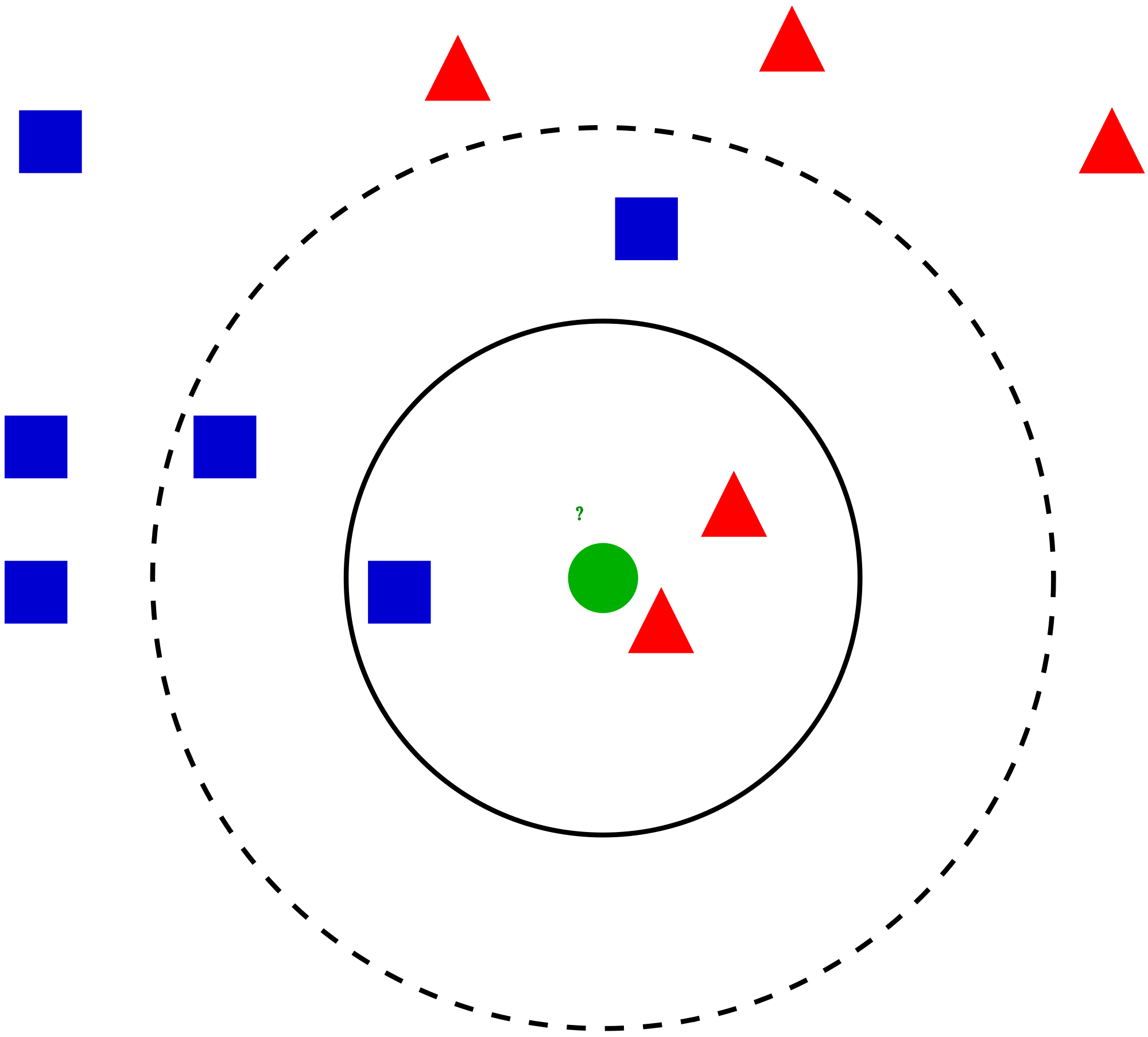
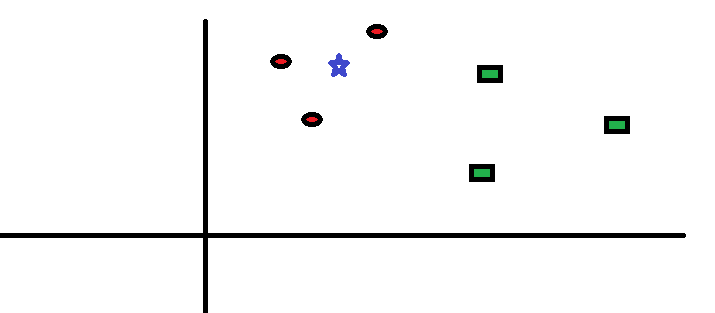Sie möchten dies herausfinden die Klasse des blauen Sterns (BS). BS kann entweder RC oder GS sein und sonst nichts. Der „K“ ist KNN-Algorithmus ist der nächste Nachbar, von dem wir abstimmen möchten. Sagen wir K = 3. Daher werden wir jetzt einen Kreis mit BS als Zentrum bilden, der genauso groß ist, dass nur drei Datenpunkte in der Ebene eingeschlossen werden Weitere Einzelheiten finden Sie im folgenden Diagramm:

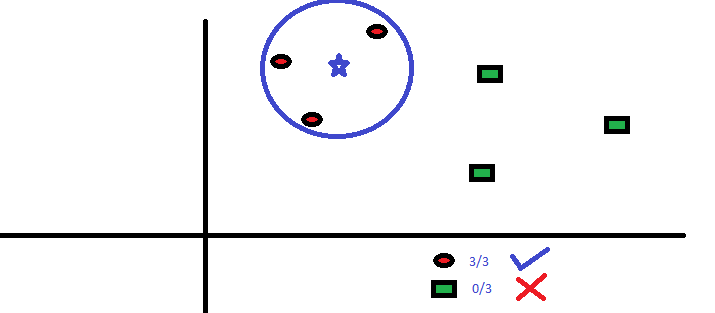Die drei nächstgelegenen Punkte zu BS sind alle RC. Mit einem guten Konfidenzniveau können wir sagen, dass die BS zur Klasse RC gehören sollte. Hier wurde die Wahl sehr offensichtlich, da alle drei Stimmen des nächsten Nachbarn zu RC gingen. Die Wahl des Parameters K ist bei diesem Algorithmus sehr wichtig Als nächstes werden wir verstehen, welche Faktoren zu berücksichtigen sind, um das beste K zu schließen.

Wie wählen wir den Faktor K aus?

Versuchen wir zunächst zu verstehen, was genau K im Algorithmus beeinflusst. Wenn wir das letzte Beispiel sehen, können wir mit einem gegebenen K-Wert Grenzen für jede Klasse setzen, da alle 6 Trainingsbeobachtungen konstant bleiben Diese Grenzen trennen RC von GS. Versuchen wir auf die gleiche Weise, die Auswirkung des Werts „K“ auf die Klassengrenzen zu sehen. Im Folgenden sind die verschiedenen Grenzen aufgeführt, die die beiden Klassen mit unterschiedlichen Werten von K trennen.

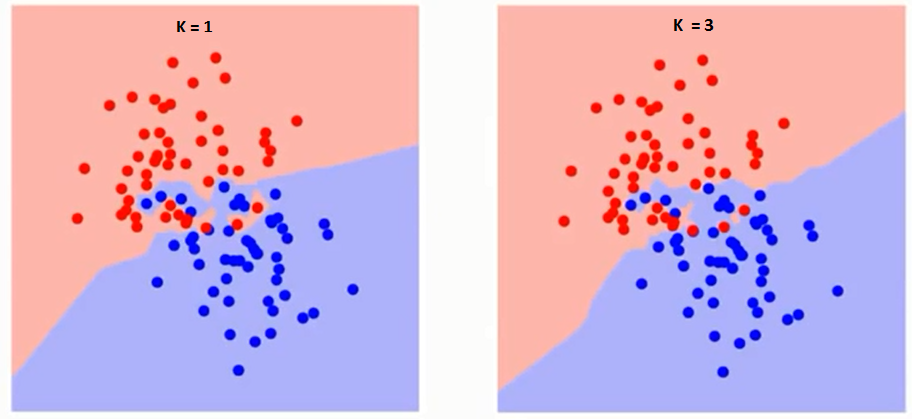
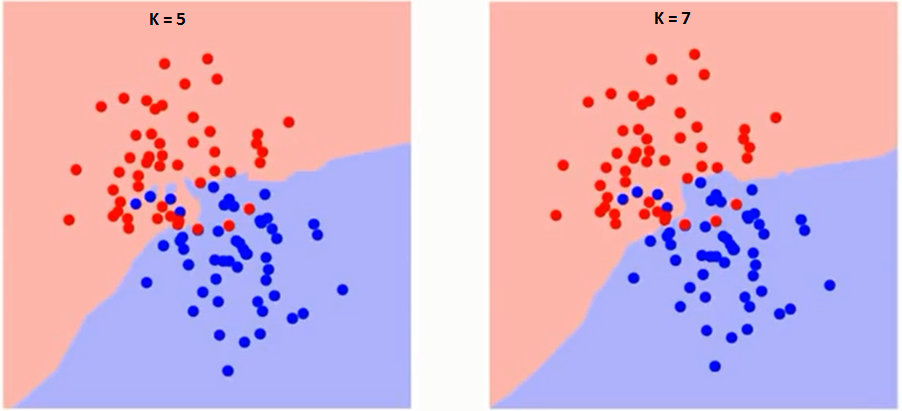
Wenn Sie genau hinschauen, können Sie das sehen Die Grenze wird mit zunehmendem Wert von K glatter. Wenn K bis unendlich ansteigt, wird es schließlich ganz blau oder ganz rot, abhängig von der Gesamtmehrheit. Die Trainingsfehlerrate und die Validierungsfehlerrate sind zwei Parameter, die wir benötigen, um auf unterschiedliche K-Werte zuzugreifen. Es folgt die Kurve für die Trainingsfehlerrate mit einem variierenden Wert von K:

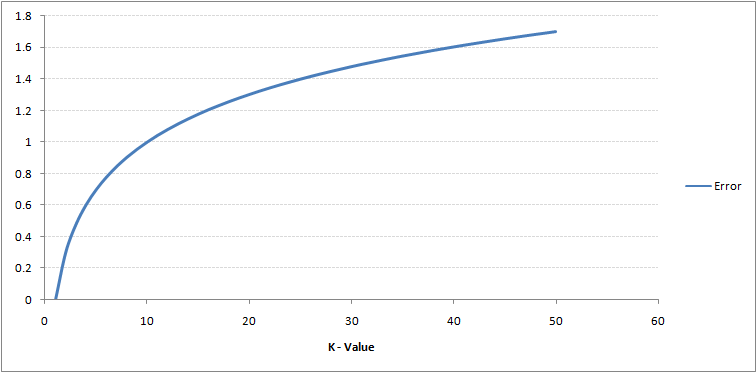Wie Sie sehen können, ist die Die Fehlerrate bei K = 1 ist für die Trainingsprobe immer Null.Dies liegt daran, dass der nächstgelegene Punkt zu einem Trainingsdatenpunkt selbst ist. Daher ist die Vorhersage mit K = 1 immer genau. Wenn die Validierungsfehlerkurve ähnlich gewesen wäre, wäre unsere Wahl von K 1 gewesen. Es folgt die Validierungsfehlerkurve mit variierendem Wert von K:

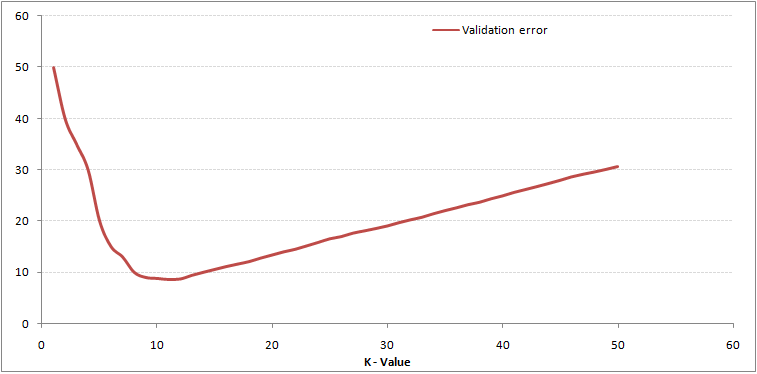Dies macht die Geschichte klarer. Bei K = 1 haben wir die Grenzen angepasst. Daher nimmt die Fehlerrate zunächst ab und erreicht ein Minimum. Nach dem Minimalpunkt steigt er mit zunehmendem K an. Um den optimalen Wert von K zu erhalten, können Sie das Training und die Validierung vom ursprünglichen Datensatz trennen. Zeichnen Sie nun die Validierungsfehlerkurve, um den optimalen Wert von K zu erhalten. Dieser Wert von K sollte für alle Vorhersagen verwendet werden.

Der obige Inhalt kann mit unserem kostenlosen Kurs – K-Nearest Neighbors ( KNN) Algorithmus in Python und R

Aufschlüsselung – Pseudocode von KNN

Wir können ein KNN-Modell implementieren, indem wir die folgenden Schritte ausführen:

1. Laden Sie die Daten
2. Initialisieren Sie den Wert von k
3. Um die vorhergesagte Klasse zu erhalten, iterieren Sie von 1 bis zur Gesamtzahl der Trainingsdatenpunkte
   1. Berechnen Sie den Abstand zwischen den Tests Daten und jede Zeile von Trainingsdaten. Hier verwenden wir die euklidische Entfernung als Entfernungsmetrik, da dies die beliebteste Methode ist. Die anderen Metriken, die verwendet werden können, sind Chebyshev, Cosinus usw.
   2. Sortieren Sie die berechneten Entfernungen in aufsteigender Reihenfolge basierend auf Entfernungswerten.
   3. Holen Sie sich die obersten k Zeilen aus dem sortierten Array
   4. Die häufigste Klasse dieser Zeilen abrufen
   5. Die vorhergesagte Klasse zurückgeben

Implementierung in Python von Grund auf

Wir werden den beliebten Iris-Datensatz zum Erstellen unseres KNN-Modells verwenden. Sie können es hier herunterladen.

Vergleich unseres Modells mit scikit-learn

Wir können sehen, dass beide Modelle dieselbe Klasse vorhergesagt haben (Iris- virginica ) und die gleichen nächsten Nachbarn (). Wir können daher den Schluss ziehen, dass unser Modell wie erwartet ausgeführt wird.

Implementierung von kNN in R

Schritt 1: Importieren der Daten

Schritt 2: Überprüfen der Daten und Berechnen der Datenzusammenfassung

Ausgabe

Schritt 3: Aufteilen der Daten

Schritt 4: Berechnen der euklidische Abstand

Schritt 5: Schreiben der Funktion zur Vorhersage von kNN

Schritt 6: Berechnen der Bezeichnung (Name) für K = 1

Ausgabe

For K=1 "Iris-virginica"

Auf die gleiche Weise können Sie für andere Werte von K berechnen.

Vergleich unserer kNN-Prädiktorfunktion mit der Bibliothek „Klasse“

Ausgabe

For K=1 "Iris-virginica"

Wir können sehen, dass beide Modelle sagten dieselbe Klasse voraus (Iris-virginica).

End Notes

Der KNN-Algorithmus ist einer der einfachsten Klassifizierungsalgorithmen Diese Einfachheit kann zu sehr wettbewerbsfähigen Ergebnissen führen. Der KNN-Algorithmus kann auch für Regressionsprobleme verwendet werden. Der einzige Unterschied Aus der diskutierten Methodik werden Durchschnittswerte der nächsten Nachbarn verwendet, anstatt von den nächsten Nachbarn abzustimmen. KNN kann in einer einzelnen Zeile in R codiert werden. Ich muss noch untersuchen, wie wir den KNN-Algorithmus in SAS verwenden können.

Fanden Sie den Artikel nützlich? Haben Sie kürzlich ein anderes Werkzeug für maschinelles Lernen verwendet? Planen Sie, KNN bei geschäftlichen Problemen einzusetzen? Wenn ja, teilen Sie uns mit, wie Sie vorhaben, dies zu tun.

Wenn Ihnen das, was Sie gerade gelesen haben, gefällt, & möchten Sie Ihr analytisches Lernen fortsetzen, abonnieren Sie unser E-Mails, folgen Sie uns auf Twitter oder mögen Sie unsere Facebook-Seite.