Was ist der BFS-Algorithmus (Breitensuche)?
Die Breitensuche (BFS) ist ein Algorithmus, der zum Zeichnen von Daten oder zum Suchen von Bäumen oder zum Durchlaufen von Strukturen verwendet wird. Die vollständige Form von BFS ist die Breitensuche.
Der Algorithmus besucht und markiert effizient alle Schlüsselknoten in einem Diagramm in einer genauen Breite. Dieser Algorithmus wählt einen einzelnen Knoten (Anfangs- oder Quellpunkt) in einem Diagramm aus und besucht dann alle Knoten neben dem ausgewählten Knoten. Denken Sie daran, dass BFS nacheinander auf diese Knoten zugreift.
Sobald der Algorithmus den Startknoten besucht und markiert, bewegt er sich zu den nächsten nicht besuchten Knoten und analysiert diese. Nach dem Besuch werden alle Knoten markiert. Diese Iterationen werden fortgesetzt, bis alle Knoten des Diagramms erfolgreich besucht und markiert wurden.
In diesem Algorithmus-Tutorial lernen Sie:
- Was ist der BFS-Algorithmus (Breadth-First Search)?
- Was sind Graph-Durchquerungen?
- Die Architektur des BFS-Algorithmus
- Warum benötigen wir den BFS-Algorithmus?
- Wie funktioniert der BFS-Algorithmus?
- Beispiel eines BFS-Algorithmus
- Regeln des BFS-Algorithmus
- Anwendungen des BFS-Algorithmus
Was sind Graph-Traversen?
Eine Diagrammdurchquerung ist eine häufig verwendete Methode zum Lokalisieren der Scheitelpunktposition im Diagramm. Es handelt sich um einen erweiterten Suchalgorithmus, mit dem der Graph schnell und präzise analysiert und die Reihenfolge der besuchten Scheitelpunkte markiert werden kann. Mit diesem Prozess können Sie schnell jeden Knoten in einem Diagramm besuchen, ohne in einer Endlosschleife eingeschlossen zu sein.
Die Architektur des BFS-Algorithmus
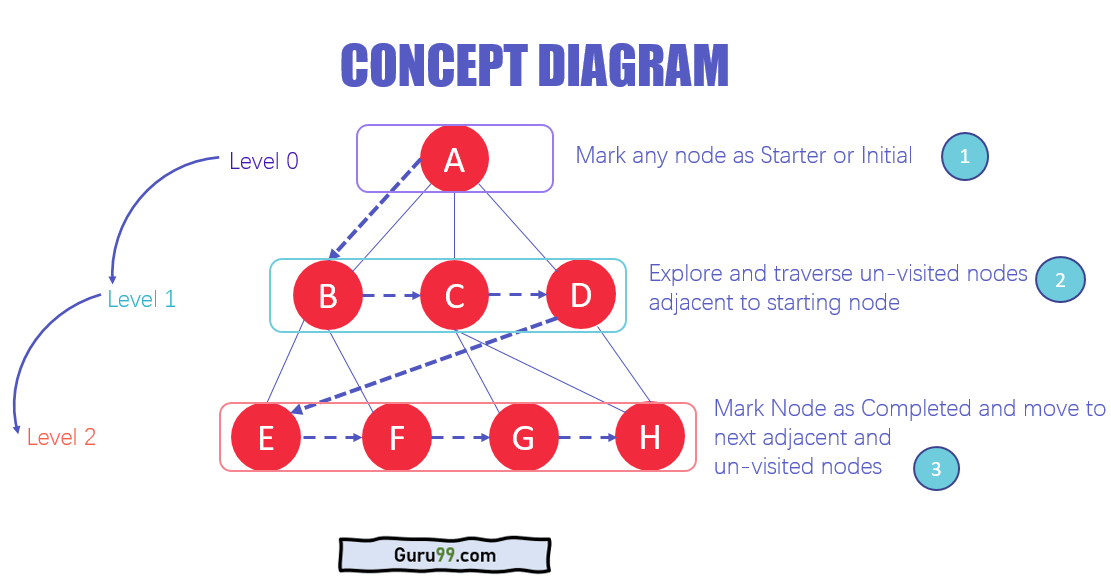
- In den verschiedenen Datenebenen können Sie einen beliebigen Knoten als Startpunkt markieren oder Anfangsknoten, um mit dem Durchlaufen zu beginnen. Das BFS besucht den Knoten und markiert ihn als besucht und stellt ihn in die Warteschlange.
- Nun besucht das BFS die nächsten und nicht besuchten Knoten und markiert sie. Diese Werte werden auch zur Warteschlange hinzugefügt. Die Warteschlange funktioniert nach dem FIFO-Modell.
- Auf ähnliche Weise werden die verbleibenden nächsten und nicht besuchten Knoten im Diagramm markiert analysiert und der Warteschlange hinzugefügt. Diese Elemente werden als empfangen aus der Warteschlange gelöscht und als Ergebnis gedruckt.
Warum benötigen wir den BFS-Algorithmus?
Es gibt zahlreiche Gründe, den BFS-Algorithmus für die Suche nach Ihrem Datensatz zu verwenden. Einige der wichtigsten Aspekte, die diesen Algorithmus zu Ihrer ersten Wahl machen, sind:
- BFS ist nützlich, um die Knoten in einem Diagramm zu analysieren und den kürzesten Weg zum Durchlaufen dieser zu konstruieren.
- BFS kann in der kleinsten Anzahl von Iterationen ein Diagramm durchlaufen.
- Die Architektur des BFS-Algorithmus ist einfach und robust.
- Das Ergebnis des BFS-Algorithmus weist im Vergleich zu anderen Algorithmen eine hohe Genauigkeit auf.
- BFS-Iterationen sind nahtlos und es besteht keine Möglichkeit, dass dieser Algorithmus in ein Endlosschleifenproblem gerät.
Wie funktioniert der BFS-Algorithmus?
Beim Durchlaufen von Graphen muss der Algorithmus jeden einzelnen nicht besuchten Knoten in einer baumartigen Struktur besuchen, überprüfen und / oder aktualisieren. Diagrammdurchläufe werden nach der Reihenfolge kategorisiert, in der sie die Knoten im Diagramm besuchen.
Der BFS-Algorithmus startet die Operation vom ersten oder Startknoten in einem Diagramm und durchläuft sie gründlich. Sobald der ursprüngliche Knoten erfolgreich durchlaufen wurde, wird der nächste nicht durchquerte Scheitelpunkt im Diagramm besucht und markiert.
Daher können Sie sagen, dass alle Knoten neben dem aktuellen Scheitelpunkt in der ersten Iteration besucht und durchlaufen werden. Eine einfache Warteschlangenmethode wird verwendet, um die Funktionsweise eines BFS-Algorithmus zu implementieren. Sie besteht aus den folgenden Schritten:
Schritt 1)

Jeder Scheitelpunkt oder Knoten im Diagramm ist bekannt. Sie können den Knoten beispielsweise als V markieren.
Schritt 2)

Wenn auf den Scheitelpunkt V nicht zugegriffen wird, fügen Sie den Scheitelpunkt V in die BFS-Warteschlange ein.
Schritt 3)

Starten Sie die BFS-Suche und markieren Sie nach Abschluss Vertex V als besucht.
Schritt 4)

Die BFS-Warteschlange befindet sich noch nicht leer, entfernen Sie daher den Scheitelpunkt V des Diagramms aus der Warteschlange.
Schritt 5)

Ruft alle verbleibenden Scheitelpunkte ab in dem Diagramm, das neben dem Scheitelpunkt V liegt
Schritt 6)

Sagen wir für jeden benachbarten Scheitelpunkt V1, falls er noch nicht besucht wurde, und fügen Sie V1 zur BFS-Warteschlange hinzu.
Schritt 7)

BFS besucht V1 und markiert es als besucht und löscht es aus der Warteschlange.
Beispiel für einen BFS-Algorithmus
Schritt 1)

Sie haben ein Diagramm von sieben Zahlen im Bereich von 0 bis 6.
Schritt 2)

0 oder Null wurde als Wurzelknoten markiert.
Schritt 3)

0 wird besucht, markiert und in die Warteschlangendatenstruktur eingefügt.
Schritt 4)
Die verbleibenden 0 benachbarten und nicht besuchten Knoten werden besucht, markiert und in die Warteschlange eingefügt.
Schritt 5)

Durchlaufiterationen werden wiederholt, bis alle Knoten besucht sind.
Regeln des BFS-Algorithmus
Hier sind wichtige Regeln für die Verwendung des BFS-Algorithmus:
- Eine Warteschlangen-Datenstruktur (FIFO-First in First Out) wird von BFS verwendet.
- Sie markieren jeden Knoten im Diagramm als root und beginnen, die Daten von ihm zu durchlaufen.
- BFS durchläuft alle Knoten im Diagramm und löscht sie weiterhin als abgeschlossen.
- BFS besucht einen benachbarten nicht besuchten Knoten, markiert ihn als erledigt und fügt ihn in eine Warteschlange ein.
- Entfernt den vorherigen Scheitelpunkt aus der Warteschlange, falls kein benachbarter Scheitelpunkt gefunden wird.
- Der BFS-Algorithmus iteriert, bis alle Scheitelpunkte im Diagramm erfolgreich durchlaufen und als abgeschlossen markiert wurden.
- Beim Durchlaufen von Daten von einem Knoten werden keine Schleifen durch BFS verursacht.
Anwendungen des BFS-Algorithmus
Nehmen wir a Schauen Sie sich einige der realen Anwendungen an, bei denen eine Implementierung des BFS-Algorithmus sehr effektiv sein kann.
- Ungewichtete Diagramme: Der BFS-Algorithmus kann auf einfache Weise den kürzesten Pfad und einen minimalen Spanning Tree erstellen, um alle zu besuchen Die Eckpunkte des Diagramms werden in kürzester Zeit mit hoher Genauigkeit erstellt.
- P2P-Netzwerke: BFS kann implementiert werden, um alle nächsten oder benachbarten Knoten in einem Peer-to-Peer-Netzwerk zu lokalisieren. Dadurch werden die erforderlichen Daten schneller gefunden
- Webcrawler: Suchmaschinen oder Webcrawler können mithilfe von BFS problemlos mehrere Indexebenen erstellen. Die BFS-Implementierung beginnt bei der Quelle, der Webseite, und besucht dann alle Links von dieser Quelle .
- Navigationssysteme: BFS kann dabei helfen, alle benachbarten Standorte vom Haupt- oder Quellstandort aus zu finden.
- Network Broadcast ing: Ein gesendetes Paket wird vom BFS-Algorithmus geleitet, um alle Knoten zu finden und zu erreichen, für die es die Adresse hat.
Zusammenfassung
- Eine Diagrammdurchquerung ist ein eindeutiger Prozess, bei dem der Algorithmus jeden einzelnen nicht besuchten Knoten in a besuchen, überprüfen und / oder aktualisieren muss baumartige Struktur. Der BFS-Algorithmus arbeitet nach einem ähnlichen Prinzip.
- Der Algorithmus ist nützlich, um die Knoten in einem Diagramm zu analysieren und den kürzesten Weg zum Durchlaufen dieser Knoten zu konstruieren.
- Der Algorithmus durchläuft den Graphen in der kleinsten Anzahl von Iterationen und in kürzester Zeit.
- BFS wählt einen einzelnen Knoten (Anfangs- oder Quellpunkt) in einem Diagramm aus und besucht dann alle Knoten neben dem ausgewählten Knoten. BFS greift nacheinander auf diese Knoten zu.
- Die besuchten und markierten Daten werden von BFS in eine Warteschlange gestellt. Eine Warteschlange arbeitet nach dem Prinzip „First In First Out“. Daher wird das zuerst im Diagramm platzierte Element zuerst gelöscht und als Ergebnis gedruckt.
- Der BFS-Algorithmus kann niemals in eine Endlosschleife geraten.
- Aufgrund seiner hohen Präzision und robusten Implementierung wird BFS in mehreren realen Lösungen wie P2P-Netzwerken, Webcrawlern usw. verwendet. und Network Broadcasting.