Wie ändert sich der Druck mit der Volumenänderung während der adiabatischen Expansion und Kompression in einem idealen Gas? Diese Seite ist ein Anhang zu unserer Diskussion über Sound. Luft mit atmosphärischem Druck ist ein nahezu ideales Gas, und die Schallübertragung in Luft ist für normale Frequenzen und Übertragungsentfernungen nahezu adiabatisch. (Wir kehren unten zu dieser Annahme zurück.)
Der erste Hauptsatz der Thermodynamik bezieht die Änderung der inneren Energie dU auf die von einem System geleistete Arbeit dW und die dazu hinzugefügte Wärme dQ.
dU = dQ – dW
Per Definition wird in einem adiabatischen Prozess die Wärme ausgetauscht dQ = 0. Wenn Sie dies in das erste Gesetz einsetzen und neu anordnen, erhalten Sie
0 = dQ = dU + dW
Der zweite Term ist einfach: Die Arbeit, die dW leistet, wenn ein System sein Volumen V um dV ändert, ist PdV.
Der erste Begriff kann sich auf die spezifische Wärme beziehen, die als die pro Temperaturänderungseinheit pro Mol Substanz zugeführte Wärme definiert ist. Wenn wir Wärme mit konstantem Volumen hinzufügen, dehnt sich das Gas nicht aus und funktioniert daher nicht. Die hinzugefügte Wärme erhöht also die innere Energie U. Daraus folgt diese Definition, dass die spezifische Wärme bei konstantem Volumen , wobei n die Anzahl der Mol ist. Daher
Nun lautet die Zustandsgleichung eines idealen Gases
nRT = PV ( ii)
wobei R die Gaskonstante ist. Die Verwendung von Derivaten ergibt
Wir können nun die Gleichungen (i) und (iii) kombinieren, um T. (i) zu eliminieren. und (ii) geben jeweils diese Ausdrücke für ncv dT an:
Das Sammeln der PdV- und VdP-Begriffe ergibt
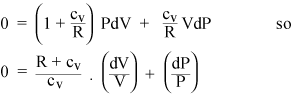
Wenn nun das Gas ideal ist, ist seine innere Energie alle kinetisch, so dass die innere Energie U nur von T abhängt. Aus der Zustandsgleichung eines idealen Gases (ii) können wir berechnen die Arbeit dW bei konstantem Druck: Es ist nur PdV = nRdT. Wenn wir also einem Gas mit konstantem Druck Wärme hinzufügen, müssen wir RdT für jedes Mol Gas zusätzlich erwärmen, über die Wärme hinaus, die wir bei konstantem Volumen hinzufügen müssen. Die spezifische Wärme eines idealen Gases bei konstantem Druck beträgt also nur cP = cv + R. Das Verhältnis der spezifischen Wärme wird mit einem Standardsymbol versehen:
. Wir haben also
(iv)
Dies ist das Hauptergebnis, das wir zur Diskussion von Schallwellen benötigen: Wir haben gerade gezeigt, dass die proportionale Druckänderung das γ-fache der proportionalen Volumenänderung oder das γ-fache der proportionalen Dichteänderung beträgt.
Lassen Sie uns hier jedoch nicht aufhören, da wir nur wenige Zeilen von einem wichtigen Ergebnis entfernt sind. Wir wissen, dass d (ln x) = dx / x (siehe Kalkül für einen Beweis). Also können wir schreiben die vorhergehende Gleichung lautet
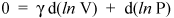
und ordnen Sie es neu an, um
(v)
Daher für einen adiabatischen Prozess in einem idealen Gas
. (vi)
Bei der Reflexion stimmen Sie zu, dass cP > cV: At konstantes Volumen, alle th Die Wärme, die Sie einbringen, erhöht die innere Energie und damit die Temperatur. Bei konstantem Druck müssen Sie nicht nur die Wärme einbringen, die die innere Energie erhöht, sondern auch eine Wärmemenge, die der Arbeit entspricht, die bei Wärmeausdehnung des Systems ausgeführt wird. Für Luft beträgt γ etwa 1,4.
Natürlich können wir jetzt (vi) aus der Zustandsgleichung (ii) ersetzen, um zu sehen, wie P und T oder T und V für einen adiabatischen Prozess zusammenhängen.
Wann ist Schall adiabatisch?
Wir haben oben erwähnt, dass „die Schallübertragung in Luft für normale Frequenzen und Übertragungsentfernungen nahezu adiabatisch ist“. Wann schlägt dies fehl? Bei den Druckmaxima in einer Schallwelle ist die Temperatur hoch. Wir erwarten daher, dass etwas Wärme in die benachbarten Druckminima diffundiert. Natürlich bleibt in einer halben Periode einer Schallwelle nicht viel Zeit, damit Wärme eine halbe Wellenlänge diffundiert. Die Zeit, die die Wärme benötigt, um zu diffundieren, ist jedoch das Quadrat der Entfernung. Daher ist dieser Prozess für hohe Frequenzen weniger vernachlässigbar, da die kürzere halbe Wellenlänge die kürzere halbe Periode mehr als kompensiert. Diese Diffusion entzieht der Welle mechanische Energie, insbesondere bei hohen Frequenzen, und der Effekt nimmt mit der Übertragungsentfernung zu.Aus diesem Grund (und manchmal auch aus anderen Gründen) sind entfernte Geräusche nicht nur weniger laut, sondern auch weniger hell als nahe Geräusche.