Das Verhältnis zwischen Druck und Volumen: Boyles Gesetz
Wenn der Druck auf ein Gas zunimmt, nimmt das Volumen des Gases ab, weil die Gaspartikel enger zusammengedrückt werden. Umgekehrt nimmt das Gasvolumen zu, wenn der Druck auf ein Gas abnimmt, weil das Gaspartikel können sich jetzt weiter auseinander bewegen. Wetterballons werden größer, wenn sie durch die Atmosphäre in Bereiche mit niedrigerem Druck aufsteigen, da das Gasvolumen zugenommen hat, dh das atmosphärische Gas übt weniger Druck auf die Oberfläche des Ballons aus Das innere Gas dehnt sich aus, bis der interne und der externe Druck gleich sind.
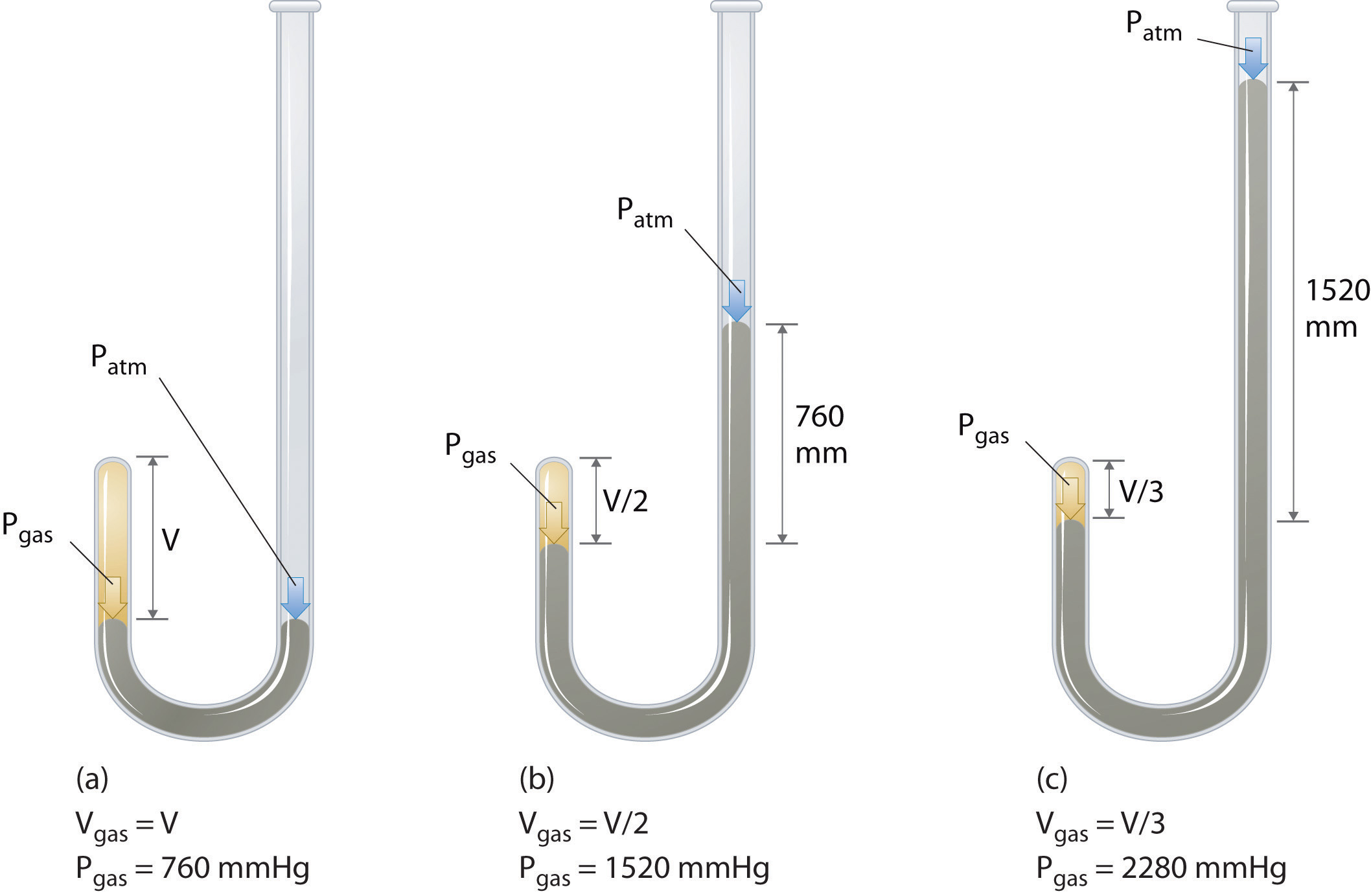
Der irische Chemiker Robert Boyle (1627–1691) führte einige der frühesten Experimente durch, die den quantitativen Zusammenhang zwischen Druck und Volumen von ein Gas. Boyle verwendete ein J-förmiges Rohr, das teilweise mit Quecksilber gefüllt war, wie in Abbildung \ (\ PageIndex {1} \) gezeigt. Bei diesen Experimenten wird eine kleine Menge eines Gases oder einer Luft über der Quecksilbersäule eingeschlossen und ihr Volumen bei Atmosphärendruck und konstanter Temperatur gemessen. Dann wird mehr Quecksilber in den offenen Arm gegossen, um den Druck auf die Gasprobe zu erhöhen. Der Druck auf das Gas ist der atmosphärische Druck plus der Höhenunterschied der Quecksilbersäulen, und das resultierende Volumen wird gemessen. Dieser Vorgang wird wiederholt, bis entweder im offenen Arm kein Platz mehr ist oder das Gasvolumen zu klein ist, um genau gemessen zu werden. Daten wie die aus einem von Boyles eigenen Experimenten können auf verschiedene Arten aufgezeichnet werden (Abbildung \ (\ PageIndex {2} \)). Eine einfache Darstellung von \ (V \) gegen \ (P \) ergibt eine Kurve, die als Hyperbel bezeichnet wird, und zeigt eine umgekehrte Beziehung zwischen Druck und Volumen: Wenn der Druck verdoppelt wird, nimmt das Volumen um den Faktor zwei ab. Diese Beziehung zwischen den beiden Größen wird wie folgt beschrieben:
\
Das Teilen beider Seiten durch \ (P \) ergibt eine Gleichung, die die umgekehrte Beziehung zwischen \ (P \) und \ veranschaulicht. (V \):
\
oder
\
wobei das Symbol ∝ gelesen wird „ist proportional zu“. Ein Diagramm von V gegen 1 / P ist somit eine gerade Linie, deren Steigung gleich der Konstante in den Gleichungen \ (\ ref {10.3.1} \) und \ (\ ref {10.3.3} \) ist Die Gleichung \ (\ ref {10.3.1} \) von V anstelle von P ergibt eine ähnliche Beziehung zwischen P und 1 / V. Der numerische Wert der Konstante hängt von der im Experiment verwendeten Gasmenge und von der Temperatur ab, bei der Die Experimente werden durchgeführt. Diese Beziehung zwischen Druck und Volumen ist nach ihrem Entdecker als Boylesches Gesetz bekannt und kann wie folgt angegeben werden: Bei konstanter Temperatur ist das Volumen einer festen Menge eines Gases umgekehrt proportional zu seinem Druck Das Gesetz in der Praxis ist in Abbildung \ (\ PageIndex {2} \) dargestellt.
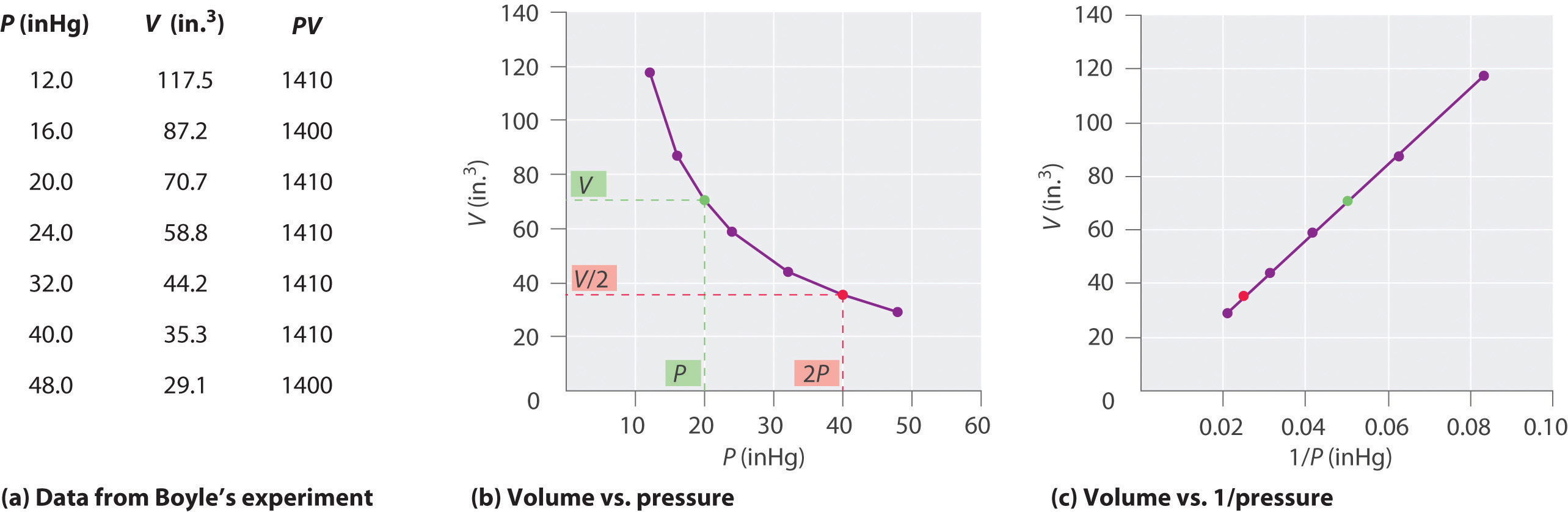
Bei konstanter Temperatur ist das Volumen einer festen Menge eines Gases umgekehrt proportional zu seinem Druck