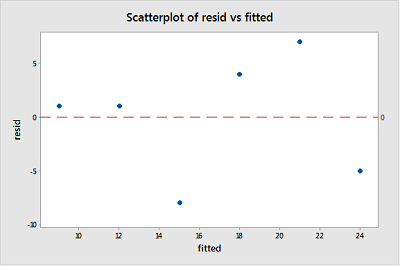
Bei der Durchführung einer Residuenanalyse wird am häufigsten ein „Residuen versus Anpassungsdiagramm“ erstellt. Es ist ein Streudiagramm von Residuen auf der y-Achse und angepassten Werten (geschätzte Antworten) auf der x-Achse. Das Diagramm wird verwendet, um Nichtlinearität, ungleiche Fehlervarianzen und Ausreißer zu erkennen.
Schauen wir uns ein Beispiel an, um zu sehen, wie ein „gut erzogenes“ Restdiagramm aussieht. Einige Forscher (Urbano- Marquez et al., 1989) waren daran interessiert festzustellen, ob der Alkoholkonsum linear mit der Muskelkraft zusammenhängt oder nicht. Die Forscher maßen den gesamten Lebenszeitkonsum von Alkohol (x) an einer Zufallsstichprobe von n = 50 alkoholkranken Männern. Sie maßen auch die Stärke (y) des Deltamuskels im nicht dominanten Arm jeder Person. Ein angepasstes Liniendiagramm der resultierenden Daten (alkoholarm.txt) sieht folgendermaßen aus:
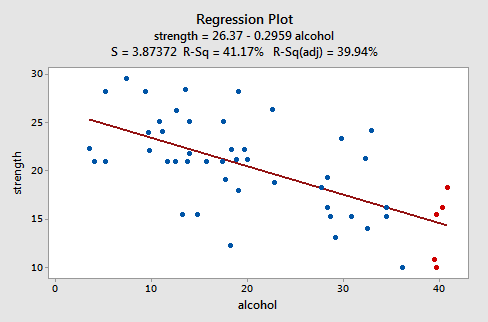
Die Darstellung legt nahe, dass es eine abnehmende lineare Beziehung zwischen Alkohol und Armstärke gibt. Es wird auch darauf hingewiesen, dass der Datensatz keine ungewöhnlichen Datenpunkte enthält. Und es zeigt, dass die Variation um die geschätzte Regressionslinie konstant ist, was darauf hindeutet, dass die Annahme gleicher Fehlervarianzen vernünftig ist.
So sehen die entsprechenden Residuen gegenüber Anpassungsdiagrammen für den Datensatz aus einfaches lineares Regressionsmodell mit Armstärke als Reaktion und Alkoholkonsum als Prädiktor:
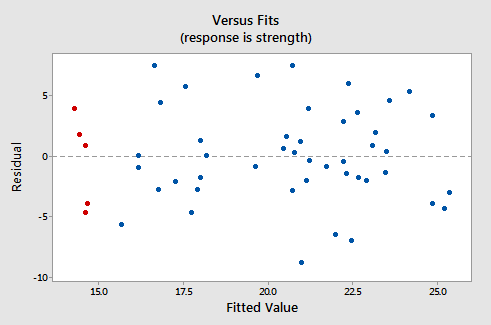
Beachten Sie, dass die Residuen wie definiert auf der y-Achse und die angepassten Werte auf der x-Achse erscheinen. Sie sollten in der Lage sein, auf das Streudiagramm der Daten zurückzublicken und zu sehen, wie die Datenpunkte dort den Datenpunkten im Residuen-gegen-Anpassungen-Diagramm hier entsprechen. Wenn Sie Probleme damit haben, sehen Sie sich die fünf Datenpunkte im ursprünglichen Streudiagramm an, die rot angezeigt werden. Beachten Sie, dass die vorhergesagte Reaktion (angepasster Wert) dieser Männer (deren Alkoholkonsum bei etwa 40 liegt) etwa 14 beträgt Beachten Sie auch das Muster, in dem die fünf Datenpunkte von der geschätzten Regressionslinie abweichen.
Sehen Sie sich nun an, wie und wo diese fünf Datenpunkte im Diagramm Residuen gegen Anpassungen erscheinen. Ihr angepasster Wert beträgt etwa 14 und ihre Abweichung von der Linie Residuum = 0 hat das gleiche Muster wie ihre Abweichung von der geschätzten Regressionslinie. Sehen Sie den Zusammenhang? Jeder Datenpunkt, der direkt auf die geschätzte Regressionslinie fällt, hat einen Rest von 0. Daher ist der Residuum = Die Linie 0 entspricht der geschätzten Regressionslinie.
Dieses Diagramm ist ein klassisches Beispiel für ein Diagramm mit gut erzogenen Residuen gegenüber Anpassungen. Hier sind die Merkmale eines Diagramms mit gut erzogenen Residuen gegenüber Anpassungen und was sie sind über die Angemessenheit der einfachen vorschlagen Das lineare Regressionsmodell:
- Die Residuen „springen zufällig“ um die 0-Linie. Dies legt nahe, dass die Annahme, dass die Beziehung linear ist, vernünftig ist.
- Die Residuen bilden ungefähr ein „horizontales Band“ um die 0-Linie. Dies legt nahe, dass die Varianzen der Fehlerterme gleich sind.
- Kein Residuum „hebt sich“ vom zufälligen Zufallsmuster der Residuen ab. Dies deutet darauf hin, dass es keine Ausreißer gibt.
Im Allgemeinen möchten Sie, dass Ihre Residuen- / Anpassungsdiagramme ungefähr so aussehen wie im obigen Diagramm. Vergessen Sie jedoch nicht, dass die Interpretation dieser Diagramme subjektiv ist. Ich habe die Erfahrung gemacht, dass Schüler, die zum ersten Mal Restanalysen lernen, dazu neigen, diese Diagramme zu überinterpretieren und jede Wendung als etwas potenziell Problematisches zu betrachten. Sie werden es besonders wollen Seien Sie vorsichtig, wenn Sie Residuen- und Anpassungsdiagrammen, die auf kleinen Datensätzen basieren, zu viel Gewicht beimessen. Manchmal sind die Datensätze einfach zu klein, um die Interpretation eines Residuen-Anpassungs-Diagramms sinnvoll zu machen. Keine Sorge! Mit etwas Übung lernen Sie, wie Sie diese Diagramme „lesen“.