Angenommen, Luft wird durch ein glattes rundes Rohr gepumpt, das einen konstanten Durchmesser hat, mit Ausnahme eines Abschnitts in der Mitte, in dem sich das Rohr verengt bis auf den halben Durchmesser, dann wieder breiter. Angenommen, alle Änderungen des Durchmessers finden reibungslos statt und die Luft strömt gleichmäßig durch das Rohr, ohne Wirbel oder Turbulenzen.
Übung
Wo im Rohr erwarten Sie der Druck, der am größten sein soll?
Antwort
Die meisten Leute, die dies zum ersten Mal fragten, sagen voraus, dass der Druck im schmalen Teil des Rohrs am größten sein wird. Wenn wir das Experiment tatsächlich durchführen, stellen wir durch Anbringen von Manometern an verschiedenen Stellen entlang des Rohrs intuitiv fest, dass der Luftdruck dort am niedrigsten ist, wo sich die Luft am schnellsten bewegt!

Um zu sehen, wie dies sein könnte, werden wir anwenden Die Techniken, die wir entwickelt haben, um herauszufinden, wie sich der Druck in einer stationären Flüssigkeit verändert. Denken Sie daran, dass wir ein Freikörperdiagramm für einen kleinen Flüssigkeitszylinder gezeichnet haben. Da dieser kleine Zylinder in Ruhe war, war die Gesamtkraft auf ihn Null, so dass der Nettodruck das Gewicht ausbalancierte. Betrachten Sie nun eine sich stetig bewegende Flüssigkeit. Es ist hilfreich, den Fluss zu visualisieren, indem Sie Stromlinien zeichnen, Linien, deren Richtung die Richtung ist, in die sich die Flüssigkeit an jedem Punkt bewegt.

Tatsächlich geben diese Stromlinien nicht nur Auskunft über die Richtung, in die sich die Flüssigkeit bewegt, sondern geben auch eine Vorstellung von der Geschwindigkeit. Wenn sie näher zusammenrücken, muss sich die Flüssigkeit schneller bewegen, da dieselbe Flüssigkeitsmenge fließt durch eine engere Region. Stellen Sie sich jetzt einen Luftzylinder vor, der sich entlang des Rohrs bewegt und dessen Achse parallel zur Stromlinie verläuft. Offensichtlich muss es schneller werden, wenn es in den schmalen Teil des Rohrs eintritt – da die gleiche Luftmenge durch den schmalen Teil wie der breite Teil strömt, muss es schneller gehen.
Aber wenn das kleine Der Flüssigkeitszylinder beschleunigt, er muss mit einer Kraft beaufschlagt werden, die ihn von hinten drückt.
Das Gewicht spielt hier keine Rolle, da es sich horizontal bewegt. Daher ist die einzige Kraft, die auf ihn wirkt, der Druck, und wir müssen daraus schließen, dass der Druck auf seiner Rückseite größer ist als der Druck auf seiner Vorderseite. Daher muss der Druck beim Eintritt in den schmalen Teil abfallen. Um klarer zu machen, was los ist, zeichnen wir einen ziemlich großen Zylinder:
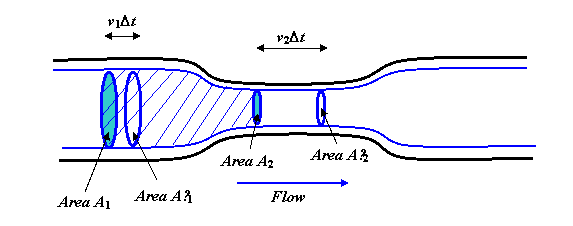
Die Flüssigkeit fließt stetig und gleichmäßig entlang das Rohr. Die dicken blauen Linien sind Stromlinien. Sie sollten sich vorstellen, das gesamte Diagramm um die Mittelachse zu drehen, um ein dreidimensionales Bild zu erhalten. Die blauen Linien würden zu einem Zylinder mit einem schmaleren „Hals“ -Abschnitt, der die Form des Rohr.
Betrachten Sie nun den Flüssigkeitskörper innerhalb der gezeigten Stromlinien, die an den beiden Enden durch die kreisförmigen Bereiche A1 und A2 abgedeckt sind. Die Flüssigkeitsströmungsrate über A1 muss der Rate von entsprechen Durchfluss über A2, da sich bei stetigem Durchfluss keine Flüssigkeit in der Mitte ansammeln kann (oder auch nicht von dort abfließt). Das Volumen, das in einer Sekunde über A1 fließt, ist v1A1 Teil. Wenn die Flüssigkeit mit beispielsweise 3 Metern pro Sekunde fließt, ist in einer Sekunde die gesamte Flüssigkeit, die sich innerhalb von 3 Metern des Bereichs A1 auf der stromaufwärtigen Seite befand, durchgeflossen.)
Also, Fluss über A1 entspricht Fluss über A2, \
(Fußnote: Es ist vielleicht erwähnenswert, dass wir implizit die Veloci annehmen ty ist an allen Stellen im Bereich A1 gleich. Jede echte Flüssigkeit hat eine gewisse Viskosität (Reibung) und bewegt sich in der Nähe der Rohrseiten langsamer als in der Mitte. Wir werden das später besprechen. Im Moment betrachten wir eine „ideale“ Flüssigkeit, den Begriff, der verwendet wird, wenn man die Viskosität ignoriert. Tatsächlich ist das Ergebnis, das wir ableiten, in Ordnung – wir hätten einen winzigen Bereich A1 weit von den Seiten entfernt nehmen können, so dass die Geschwindigkeit gewesen wäre das gleiche für das gesamte Gebiet, aber das hätte ein viel weniger klares Diagramm ergeben.)
Wir sind jetzt bereit, den Anstieg der kinetischen Energie der Flüssigkeit zu untersuchen, wenn sie in den engen Teil beschleunigt. und zu verstehen, wie die Druckdifferenz die zur Beschleunigung erforderliche Arbeit geleistet hat.
\
Die einzig mögliche Quelle für diesen Energieanstieg ist die Arbeit, die durch Druck beim Eindrücken der Flüssigkeit geleistet wird der schmale Teil.
\
Das ist also Arbeit an unserem Flüssigkeitsstück, indem die Flüssigkeit es von hinten drückt – aber das ist nicht das Ende der Geschichte, weil unser Stück Flüssigkeit selbst funktioniert, indem sie die Flüssigkeit vor sich drückt. Um also die Gesamterhöhung der Energie unseres Stücks zu ermitteln, müssen wir die externe Arbeit, die sie leistet, abziehen.Das heißt, die Gesamtarbeit, die durch Druck auf unsere Flüssigkeit geleistet wird, ist
\
, wenn man sich daran erinnert, dass \ (A_1v_1 = A_2v_2 \).
Diese Arbeit muss gleich sein die Änderung der kinetischen Energie, also
\
aus der
\
Dies ist die Bernoulli-Gleichung.
\.
Mitwirkende und Zuschreibungen
- Michael Fowler (Beams-Professor, Fachbereich Physik, Universität von Virginia)