Quando si esegue unanalisi dei residui, un “grafico dei residui rispetto agli adattamenti” è il grafico creato più di frequente. È un grafico a dispersione dei residui sullasse y e dei valori adattati (risposte stimate) sullasse x. Il grafico viene utilizzato per rilevare non linearità, varianze di errore ineguali e valori anomali.
Diamo unocchiata a un esempio per vedere come appare un grafico residuo “ben comportato”. Alcuni ricercatori (Urbano- Marquez, et al., 1989) erano interessati a determinare se il consumo di alcol fosse correlato linearmente o meno alla forza muscolare. I ricercatori hanno misurato il consumo totale di alcol nel corso della vita (x) su un campione casuale di n = 50 uomini alcolisti. Hanno anche misurato la forza (y) del muscolo deltoide nel braccio non dominante di ogni persona. Un grafico a linee adattate dei dati risultanti, (alcoholarm.txt), ha il seguente aspetto:
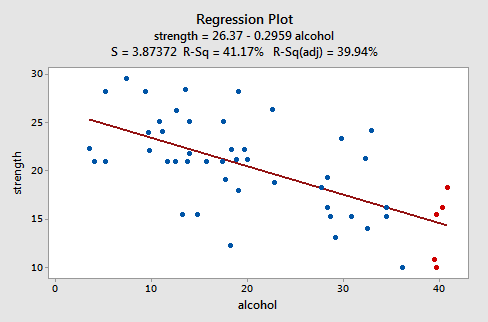
La trama suggerisce che esiste una relazione lineare decrescente tra alcol e forza delle braccia. Suggerisce inoltre che non ci siano punti dati insoliti nel set di dati. Inoltre, illustra che la variazione attorno alla retta di regressione stimata è costante, suggerendo che lipotesi di uguali varianze di errore è ragionevole.
Ecco come appare il grafico dei residui corrispondenti rispetto agli adattamenti per il set di dati “s modello di regressione lineare semplice con la forza del braccio come risposta e il livello di consumo di alcol come predittore:
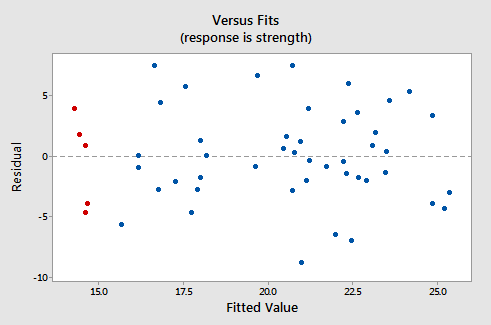
Notare che, come definito, i residui vengono visualizzati sullasse y ei valori adattati vengono visualizzati sullasse x. Dovresti essere in grado di guardare indietro al grafico a dispersione dei dati e vedere come i punti dati corrispondono ai punti dati nel grafico dei residui rispetto a quelli degli adattamenti qui. Nel caso in cui tu abbia problemi a farlo, guarda i cinque punti dati nel grafico a dispersione originale che appaiono in rosso. Nota che la risposta prevista (valore adattato) di questi uomini (il cui consumo di alcol è di circa 40) è di circa 14 . Inoltre, osserva il modello in cui i cinque punti dati deviano dalla linea di regressione stimata.
Ora guarda come e dove questi cinque punti dati appaiono nel grafico dei residui rispetto agli adattamenti. Il loro valore adattato è di circa 14 e la loro deviazione dalla linea residuale = 0 condivide lo stesso modello della loro deviazione dalla linea di regressione stimata. Vedi la connessione? Qualsiasi punto dati che cade direttamente sulla linea di regressione stimata ha un residuo di 0. Pertanto, il residuo = La linea 0 corrisponde alla linea di regressione stimata.
Questo grafico è un classico esempio di un grafico dei residui ben comportati e degli accoppiamenti. Di seguito sono riportate le caratteristiche di un grafico dei residui e degli accoppiamenti ben comportati e cosa suggerire circa lappropriatezza del semplice Il modello di regressione lineare:
- I residui “rimbalzano casualmente” attorno alla linea 0. Ciò suggerisce che lipotesi che la relazione sia lineare sia ragionevole.
- I residui formano allincirca una “banda orizzontale” attorno alla linea 0. Ciò suggerisce che le varianze dei termini di errore sono uguali.
- Nessun residuo “si distingue” dal modello casuale di base dei residui. Ciò suggerisce che non ci sono valori anomali.
In generale, si desidera che i grafici dei residui e degli adattamenti abbiano un aspetto simile al grafico precedente. Non dimenticare però che linterpretazione di queste trame è soggettiva. La mia esperienza è stata che gli studenti che apprendono lanalisi residua per la prima volta tendono a interpretare eccessivamente queste trame, considerando ogni svolta e svolta come qualcosa di potenzialmente fastidioso. fare attenzione a non dare troppo peso ai grafici dei residui e degli adattamenti basati su piccoli set di dati. A volte i set di dati sono semplicemente troppo piccoli per rendere utile linterpretazione di un grafico dei residui e degli adattamenti. Non ti preoccupare! Imparerai – con la pratica – come “leggere” questi grafici.