1.3: Leffetto Bernoulli

Supponiamo che laria venga pompata in un tubo tondo liscio, che ha un diametro costante tranne che per una sezione nel mezzo dove il tubo si restringe fino a metà del diametro, quindi si allarga di nuovo. Supponi che tutte le variazioni di diametro avvengano senza intoppi e che laria fluisca costantemente lungo il tubo, senza vortici o turbolenze.

Per vedere come potrebbe essere, applicheremo le tecniche che abbiamo sviluppato per scoprire come variava la pressione in un fluido stazionario. Il modo in cui labbiamo fatto, ricorda, è stato disegnare un diagramma a corpo libero per un piccolo cilindro di fluido. Poiché questo piccolo cilindro era fermo, la forza totale su di esso era zero, quindi la pressione netta bilanciava il peso. Ora considera un fluido in costante movimento. È utile visualizzare il flusso disegnando linee di flusso, linee tali che la loro direzione sia la direzione in cui si muove il fluido in ogni punto.

In realtà, queste linee di flusso non solo ti dicono la direzione in cui si muove il fluido, ma danno anche unidea della velocità: dove si avvicinano, il fluido deve muoversi più velocemente, perché la stessa quantità di fluido scorre attraverso una regione più stretta. Immagina ora un cilindro daria che si muove lungo il tubo, il suo asse parallelo alla linea di flusso. Ovviamente, deve accelerare quando entra nella parte stretta del tubo, poiché la stessa quantità daria scorre attraverso la parte stretta come la parte larga, deve andare più veloce.

Ma se la parte piccola il cilindro di fluido sta accelerando, deve essere azionato da una forza che lo spinge da dietro.

Il suo peso è irrilevante qui, poiché si muove orizzontalmente. Pertanto lunica forza che agisce su di esso è la pressione, e dobbiamo concludere che la pressione alla sua schiena è maggiore della pressione sul suo fronte. Pertanto la pressione deve diminuire entrando nella parte stretta. Per rendere più chiaro cosa sta succedendo, disegneremo un cilindro piuttosto grande:

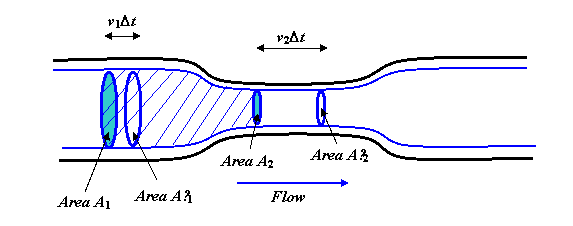
Il fluido scorre in modo regolare e regolare la pipa. Le spesse linee blu sono linee aerodinamiche, infatti dovresti immaginare di ruotare lintero diagramma attorno allasse centrale per ottenere unimmagine tridimensionale, e le linee blu diventerebbero un cilindro, con una sezione “collo” più stretta, che riecheggia la forma del .

Ora si consideri il corpo del fluido allinterno delle linee di flusso mostrate e chiuso alle due estremità dalle aree circolari A1 e A2. La velocità di flusso del fluido attraverso A1 deve essere la stessa della velocità di flusso attraverso A2, perché in un flusso costante il fluido non può accumularsi nel mezzo (o esaurirsi da lì). Il volume che scorre attraverso A1 in un secondo è v1A1. (Per vedere questo, immagina un tubo lungo e diritto senza uno stretto Se il fluido scorre a, diciamo 3 metri al secondo, in un secondo sarà passato tutto il fluido che si trovava entro 3 metri dallarea A1 sul lato a monte.)

Quindi, il flusso attraverso A1 è uguale al flusso attraverso A2, \

(Nota a piè di pagina: forse vale la pena ricordare che stiamo assumendo implicitamente che le velocità la tà è la stessa in tutti i punti dellarea A1. Qualsiasi fluido reale ha una certa viscosità (attrito) e si muoverà più lentamente vicino ai lati del tubo rispetto al centro. Ne parleremo più tardi. Per ora consideriamo un fluido “ideale”, termine usato quando si ignora la viscosità. Infatti il risultato che ne deriva è ok, avremmo potuto prendere una minuscola area A1 molto lontana dai lati, in modo che la velocità sarebbe stata lo stesso per lintera area, ma ciò avrebbe fornito un diagramma molto meno chiaro.)

Ora siamo pronti per esaminare laumento dellenergia cinetica del fluido mentre accelera nella parte stretta, e capire come la differenza di pressione ha svolto il lavoro necessario per accelerarla.

\

Lunica fonte possibile per questo aumento di energia è il lavoro svolto dalla pressione nel spingere il fluido la parte più stretta.

\

Quindi questo è il lavoro svolto sul nostro pezzo di fluido dal fluido che lo spinge da dietro, ma non è la fine della storia, perché il nostro pezzo di fluido il fluido stesso funziona spingendo il fluido di fronte ad esso, quindi per trovare laumento totale dellenergia del nostro pezzo, dobbiamo sottrarre il lavoro esterno che fa.Cioè, il lavoro totale svolto dalla pressione sul nostro fluido è

\

ricordando che \ (A_1v_1 = A_2v_2 \).

Questo lavoro svolto deve essere uguale la variazione dellenergia cinetica, quindi

\

da cui

\

Questa è lequazione di Bernoulli.

\.