A suma este rezultatul unei adunări. De exemplu, adăugând 1, 2, 3 și 4 se obține suma 10, scris
 |
(1)
|
Numerele care sunt însumate se numesc adunări sau uneori sumande. Operația de însumare poate fi, de asemenea, indicată folosind o sigmă de capital cu limite superioare și inferioare scrise deasupra și dedesubt, iar indicele indicat mai jos. De exemplu, suma de mai sus ar putea fi scrisă
 |
(2)
|
The suma unei liste de numere este implementată ca Total.
O sumă
 |
(3)
|
în care fiecare termen 
este dat de o regulă fixă (adică, 
este o fântână -secvență definită) se numește serie (finită) și dacă numărul de termeni 
este infinit, suma se numește serie infinită (sau adesea doar o „serie”). O sumă a formei
 |
(4)
|
se numește serie geometrică .
Condițiile pentru convergența unei serii pot fi determinate în limbajul Wolfram folosind SumConvergence.
Suma generală a puterii finite
 |
(5)
|
poate fi dat de expresia
 |
(6)
|
care este echivalent cu formula lui Faulhaber, unde notația 
înseamnă cantitatea din întrebarea este ridicată la puterea corespunzătoare 
și toți termenii formei 
sunt înlocuiți cu valoarea corespunzătoare Numere Bernoulli 
.
O identitate amuzantă datorată lui J. Ziegenbein (pers. com., 19 iunie 2002) rezultă din identitate
 |
(7)
|
care poate fi scris
 |
(8)
|
Prin urmare, 
, de exemplu, poate fi scris în formele echivalente
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
 |
 |
 |
(12)
|
și așa mai departe.
Teorema lui Nicomachus oferă o expresie curioasă pentru suma puterii 
.
Sumele speciale includ
 |
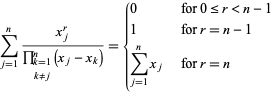(13)
|
și
 |
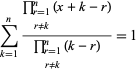(14)
|
Pentru a minimiza suma unui set de pătrate de numere 
despre un număr dat 
 |
 |
 |
(15 )
|
 |
 |
 |
(16)
|
luați derivatul.
 |
(17)
|
Rezolvarea pentru 
dă
 |
(18)
|
deci 
este minimizat când 
este setat la înseamnă.