Introducere în k-Near Neighbours: Un algoritm puternic de învățare automată (cu implementare în Python & R)

Notă: Acest articol a fost publicat inițial la 10 octombrie 2014 și actualizat la 27 martie 2018

Prezentare generală

• Înțelegeți cel mai apropiat vecin (KNN) – unul dintre cei mai populari algoritmi de învățare automată
• Aflați cum funcționează kNN în python
• Alegeți valoarea corectă a lui k în termeni simpli

Introducere

În cei patru ani din cariera mea în știința datelor, am construit peste 80% modele de clasificare și doar 15-20% modele de regresie. Aceste rapoarte pot fi mai mult sau mai puțin generalizate în întreaga industrie. Motivul care stă la baza acestei tendințe față de modelele de clasificare este că majoritatea problemelor analitice implică luarea unei decizii.

De exemplu, un client va atrage sau nu, ar trebui să ne orientăm către clientul X pentru campanii digitale, indiferent dacă clientul are un potențial ridicat sau nu, etc. Aceste analize sunt mai inteligente și direct legate de o foaie de parcurs de implementare.

În acest articol, vom vorbi despre o altă tehnică de clasificare a învățării automate folosită pe scară largă numită K-nearest neighbors (KNN). Accentul nostru se va concentra în primul rând pe modul în care funcționează algoritmul și modul în care parametrul de intrare afectează ieșirea / predicția.

Notă: persoanele care preferă să învețe prin videoclipuri pot învăța la fel prin cursul nostru gratuit – K- Cel mai apropiat algoritm de vecini (KNN) în Python și R. Și dacă sunteți un începător complet în știința datelor și învățarea automată, consultați programul nostru Certified BlackBelt –

• AI certificată & Programul ML Blackbelt +

Cuprins

• Când folosim algoritmul KNN?
• Cum funcționează Algoritmul KNN funcționează?
• Cum alegem factorul K?
• Descompunerea – Pseudo Codul KNN
• Implementarea în Python de la zero
• Comparând modelul nostru cu scikit-learn

Când folosim algoritmul KNN?

KNN poate fi utilizat pentru ambele probleme predictive de clasificare și regresie. Cu toate acestea, este mai utilizat în problemele de clasificare din industrie. Pentru a evalua orice tehnică, ne uităm, în general, la 3 aspecte importante:

1. Ușor de interpretat ieșirea

2. Timp de calcul

3. Puterea predictivă

Să luăm câteva exemple pentru a plasa KNN în scară:

Târgurile de algoritmi KNN pe toți parametrii de considerații. Este utilizat în mod obișnuit pentru interpretarea ușoară și timpul de calcul redus.

Cum funcționează algoritmul KNN?

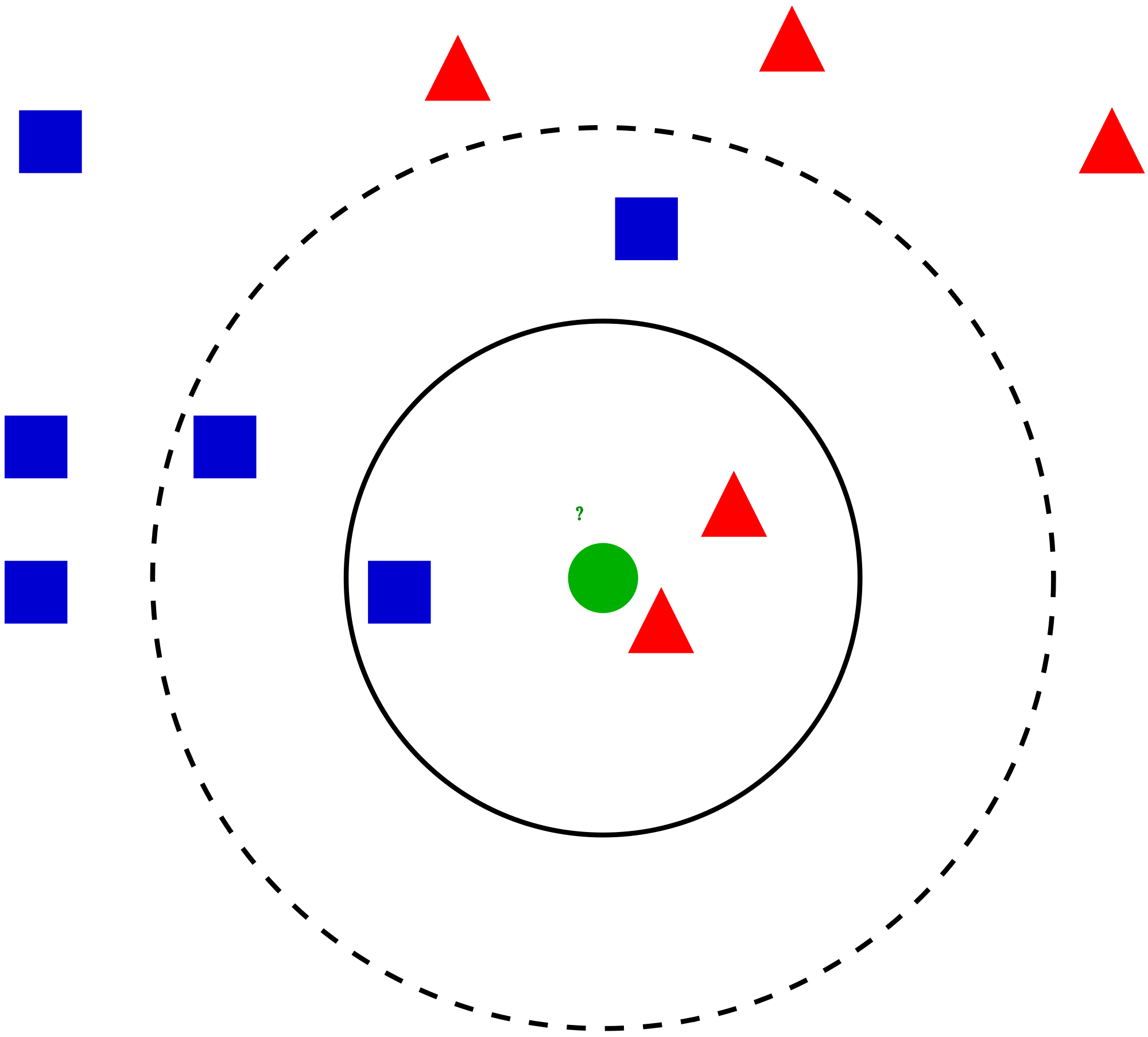
Să luăm un caz simplu la înțelegeți acest algoritm. Urmează o răspândire de cercuri roșii (RC) și pătrate verzi (GS):

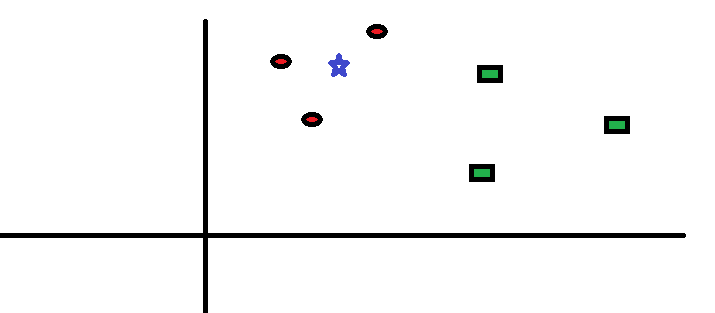Vrei să afli clasa stelei albastre (BS). BS poate fi RC sau GS și nimic altceva. Algoritmul „K” este KNN este cel mai apropiat vecin de la care dorim să votăm. Să zicem K = 3. Prin urmare, vom face acum un cerc cu BS ca centru la fel de mare ca să închidem doar trei puncte de date în plan . Consultați următoarea diagramă pentru mai multe detalii:

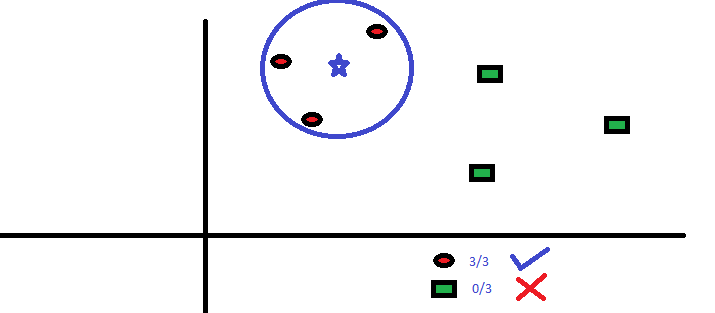Cele mai apropiate trei puncte de BS sunt toate RC. Prin urmare, cu un nivel bun de încredere, putem spune că BS ar trebui să aparțină clasei RC. Aici, alegerea a devenit foarte evidentă, deoarece toate cele trei voturi de la cel mai apropiat vecin au mers la RC. Alegerea parametrului K este foarte crucială în acest algoritm Apoi, vom înțelege care sunt factorii care trebuie luați în considerare pentru a concluziona cel mai bun K.

Cum alegem factorul K?

Mai întâi să încercăm să înțelegem ce influențează K în algoritm. Dacă vedem ultimul exemplu, având în vedere că toate cele 6 observații de antrenament rămân constante, cu o valoare K dată putem face limite pentru fiecare clasă. limitele vor separa RC de GS. În același mod, să încercăm să vedem efectul valorii „K” asupra limitelor clasei. Următoarele sunt limitele diferite care separă cele două clase cu valori diferite ale K.

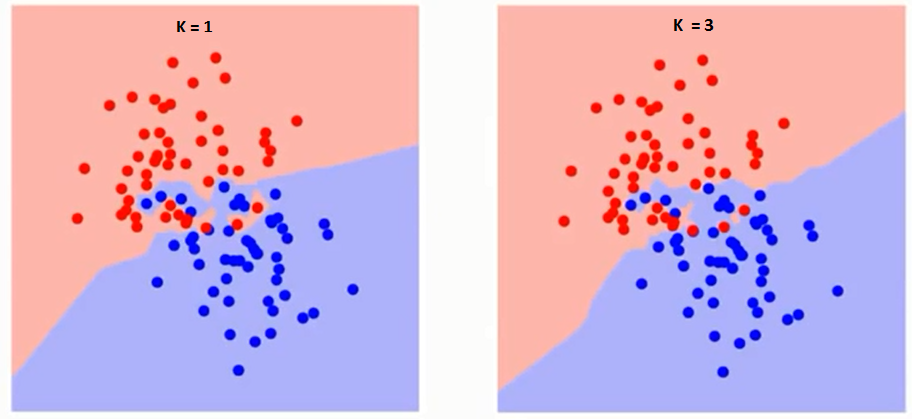
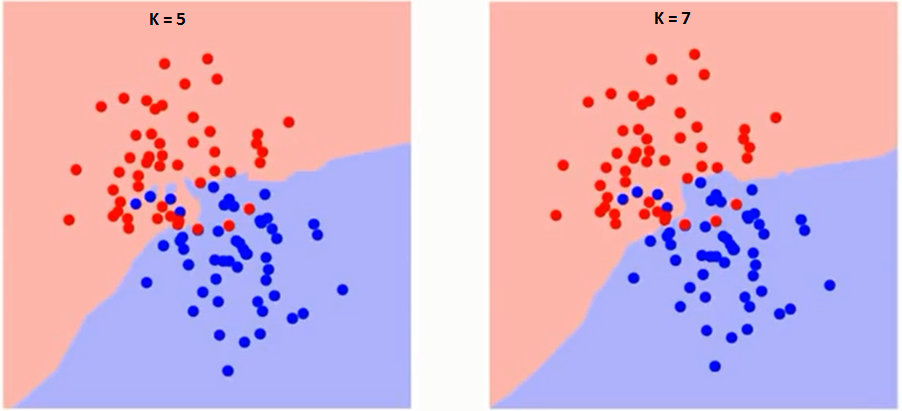
Dacă urmăriți cu atenție, puteți vedea că granița devine mai lină odată cu creșterea valorii lui K. Odată cu creșterea K la infinit, devine în cele din urmă toate albastre sau toate roșii în funcție de majoritatea totală. Urmează curba pentru rata de eroare de antrenament cu o valoare variabilă de K:

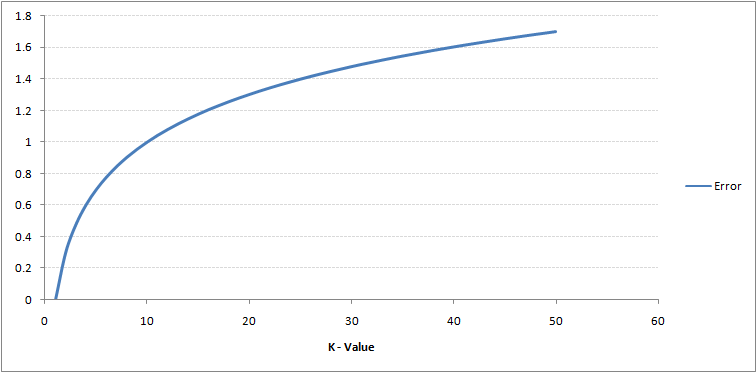După cum puteți vedea, rata de eroare la K = 1 este întotdeauna zero pentru eșantionul de antrenament.Acest lucru se datorează faptului că punctul cel mai apropiat de orice punct de date de antrenament este el însuși. Prin urmare, predicția este întotdeauna exactă cu K = 1. Dacă curba de eroare de validare ar fi fost similară, alegerea noastră pentru K ar fi fost 1. Urmează curba de eroare de validare cu valoare variabilă a K:

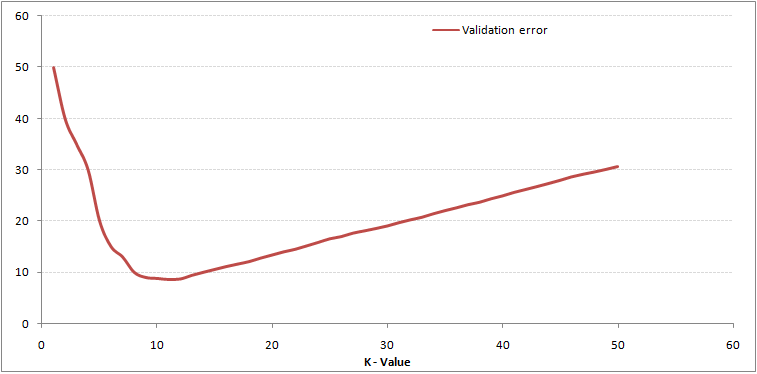Aceasta face povestea mai clară. La K = 1, depășeam limitele. Prin urmare, rata de eroare scade inițial și atinge valori minime. După punctul minim, acesta crește odată cu creșterea K. Pentru a obține valoarea optimă a lui K, puteți separa antrenamentul și validarea de setul de date inițial. Acum trasați curba de eroare de validare pentru a obține valoarea optimă a lui K. Această valoare a lui K ar trebui utilizată pentru toate predicțiile.

Conținutul de mai sus poate fi înțeles mai intuitiv folosind cursul nostru gratuit – K-Near Neighbours ( KNN) Algoritm în Python și R

Descompunerea – Pseudo Codul KNN

Putem implementa un model KNN urmând pașii de mai jos:

1. Încărcați datele
2. Initializați valoarea lui k
3. Pentru a obține clasa prezisă, iterați de la 1 la numărul total de puncte de date de antrenament
   1. Calculați distanța dintre test date și fiecare rând de date de antrenament. Aici vom folosi distanța euclidiană ca metrică a distanței noastre, deoarece este cea mai populară metodă. Celelalte valori care pot fi utilizate sunt Chebyshev, cosinus etc.
   2. Sortați distanțele calculate în ordine crescătoare pe baza valorilor distanței
   3. Obțineți k rânduri de sus din matricea sortată >
   4. Obțineți cea mai frecventă clasă a acestor rânduri
   5. Reveniți la clasa prezisă

Implementarea în Python de la zero

Vom folosi popularul set de date Iris pentru construirea modelului nostru KNN. O puteți descărca de aici.

Comparând modelul nostru cu scikit-learn

Putem vedea că ambele modele au prezis aceeași clasă („Iris- virginica ) și aceiași vecini cei mai apropiați (). Prin urmare, putem concluziona că modelul nostru rulează conform așteptărilor.

Implementarea kNN în R

Pasul 1: Importul datelor

Pasul 2: Verificarea datelor și calcularea rezumatului datelor

Ieșire

Pasul 3: Împărțirea datelor

Pasul 4: Calcularea distanța euclidiană

Pasul 5: Scrierea funcției pentru a prezice kNN

Pasul 6: Calcularea etichetei (Nume) pentru K = 1

Ieșire

For K=1 "Iris-virginica"

În același mod, puteți calcula pentru alte valori ale lui K.

Compararea funcției noastre predictor kNN cu biblioteca „Class”

Ieșire

For K=1 "Iris-virginica"

Putem vedea că ambele modelele au prezis aceeași clasă („Iris-virginica”).

Note finale

Algoritmul KNN este unul dintre cele mai simple algoritmi de clasificare. o astfel de simplitate, poate da rezultate extrem de competitive. Algoritmul KNN poate fi folosit și pentru probleme de regresie. Singura diferență din metodologia discutată se vor folosi medii ale celor mai apropiați vecini, mai degrabă decât votarea celor mai apropiați vecini. KNN poate fi codat într-o singură linie pe R. Încă trebuie să explorez cum putem folosi algoritmul KNN pe SAS.

Ați găsit articolul util? Ați folosit recent vreun alt instrument de învățare automată? Aveți de gând să utilizați KNN în vreo problemă de afaceri? Dacă da, împărtășiți cu noi cum intenționați să faceți acest lucru.

Dacă vă place ceea ce tocmai ați citit & doriți să continuați învățarea analizei, abonați-vă la e-mailuri, urmați-ne pe twitter sau apreciați pagina noastră de facebook.