Cum variază presiunea cu variația volumului în timpul expansiunii și compresiei adiabatice într-un gaz ideal? Această pagină este o anexă la discuția noastră despre sunet. Aerul la presiunea atmosferică este un gaz aproape ideal, iar transmisia sunetului în aer este aproape de adiabatic pentru frecvențe și distanțe de transmisie normale. (Revenim la această ipoteză mai jos.)
Prima lege a termodinamicii corelează schimbarea energiei interne dU cu munca dW realizată de un sistem și căldura dQ adăugată la acesta.
dU = dQ – dW
Prin definiție, într-un proces adiabatic, căldura schimbată dQ = 0. Înlocuind acest lucru în prima lege și rearanjând se obține
0 = dQ = dU + dW
Al doilea termen este ușor: munca efectuată dW atunci când un sistem își schimbă volumul V cu dV este PdV.
Primul termen poate fi legat de căldura specifică, care este definită ca căldura adăugată pe unitatea de modificare a temperaturii per mol de substanță. Dacă adăugăm căldură la volum constant, atunci gazul nu se extinde și nu funcționează. Deci căldura adăugată crește energia internă U. Deci, urmează acea definiție că căldura specifică la volum constant este ![]() , unde n este numărul de alunițe. Prin urmare,
, unde n este numărul de alunițe. Prin urmare,
Acum ecuația de stare a unui gaz ideal este
nRT = PV ( ii)
unde R este constanta gazului. Luarea derivatelor dă
Acum putem combina ecuațiile (i) și (iii) pentru a elimina T. (i) și (ii) oferă respectiv aceste expresii pentru ncv dT:
Colectarea termenilor PdV și VdP dă
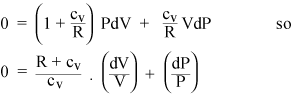
Acum, dacă gazul este ideal, energia sa internă este cinetică, deci energia internă U depinde doar de T. Din ecuația de stare a unui gaz ideal (ii), putem calcula munca dW realizată la presiune constantă: este doar PdV = nRdT. Deci, dacă adăugăm căldură unui gaz la presiune constantă, trebuie să încălzim suplimentar RdT pentru fiecare mol de gaz, dincolo de căldură ar trebui să adăugăm la volum constant. Deci căldura specifică a unui gaz ideal la presiune constantă este doar cP = cv + R. Raportul dintre căldurile specifice este dat cu un simbol standard:
. Deci avem
(iv)
Acesta este rezultatul principal pe care trebuie să-l discutăm despre undele sonore: tocmai am arătat că schimbarea proporțională a presiunii este – γ ori schimbarea proporțională a volumului sau γ ori schimbarea proporțională a densității.
Să nu ne oprim totuși aici, pentru că suntem la doar câteva linii distanță de un rezultat important. Știm că d (ln x) = dx / x (a se vedea calculul pentru o dovadă). Deci putem scrie ecuația precedentă ca
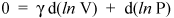
și rearanjați-l pentru a da
(v)
Prin urmare, pentru un proces adiabatic într-un gaz ideal,
. (vi)
La reflecție, veți fi de acord că cP > cV: volum constant, tot al Căldura pe care o introduceți duce la creșterea energiei interne și, astfel, la creșterea temperaturii. La presiune constantă, trebuie să introduceți nu numai căldura care ridică energia internă, ci și o cantitate de căldură egală cu munca depusă atunci când sistemul este supus expansiunii termice. Pentru aer, γ este de aproximativ 1,4.
Desigur, putem înlocui acum în (vi) din ecuația stării (ii) pentru a vedea cum P și T sau T și V sunt legate pentru un proces adiabatic.
Când sunetul este adiabatic?
Am menționat mai sus că „transmisia sunetului în aer este aproape de adiabatic pentru frecvențe și distanțe de transmisie normale”. Când eșuează acest lucru? La presiunea maximă într-o undă sonoră, temperatura este ridicată. Deci, ne așteptăm ca o anumită căldură să difuzeze la minimele de presiune învecinate. Desigur, într-o jumătate de perioadă a unei unde sonore, nu există prea mult timp pentru căldură să difuzeze o jumătate de lungime de undă. Cu toate acestea, timpul necesar pentru difuzarea căldurii merge ca pătratul distanței. Deci, acest proces este mai puțin neglijabil pentru frecvențele înalte, deoarece jumătatea mai mică decât lungimea de undă compensează mai mult decât jumătatea mai scurtă. Această difuzie scoate energia mecanică din undă, în special la frecvențe înalte, iar efectul crește odată cu distanța de transmisie.Din acest motiv (și uneori și altele), sunetele îndepărtate nu sunt doar mai puțin puternice, ci și mai puțin strălucitoare decât cele apropiate.