Algoritm Breadth First Search (BFS) cu EXEMPLU

Ce este algoritmul BFS (Breadth-First Search)?

Breadth-first search (BFS) este un algoritm care este utilizat pentru graficarea datelor, căutarea în arborele sau structurile de traversare. Forma completă a BFS este prima căutare a lățimii.

Algoritmul vizitează și marchează în mod eficient toate nodurile cheie într-un grafic într-o manieră exactă în funcție de latură. Acest algoritm selectează un singur nod (punct inițial sau sursă) într-un grafic și apoi vizitează toate nodurile adiacente nodului selectat. Amintiți-vă, BFS accesează aceste noduri unul câte unul.

Odată ce algoritmul vizitează și marchează nodul de pornire, acesta se deplasează spre cele mai apropiate noduri nevizitate și le analizează. Odată vizitate, toate nodurile sunt marcate. Aceste iterații continuă până când toate nodurile grafului au fost vizitate și marcate cu succes.

În acest tutorial Algoritm, veți afla:

• Ce este Algoritmul BFS (Breadth-First Search)?
• Ce este traversarea graficului?
• Arhitectura algoritmului BFS
• De ce avem nevoie de algoritmul BFS?
• Cum funcționează algoritmul BFS?
• Exemplu de algoritm BFS
• Reguli ale algoritmului BFS
• Aplicații ale algoritmului BFS

Ce este traversarea graficului?

O traversare a graficului este o metodologie frecvent utilizată pentru localizarea poziției vârfului în grafic. Este un algoritm de căutare avansată care poate analiza graficul cu viteză și precizie, împreună cu marcarea secvenței vârfurilor vizitate. Acest proces vă permite să vizitați rapid fiecare nod dintr-un grafic fără a fi blocat într-o buclă infinită.

Arhitectura algoritmului BFS

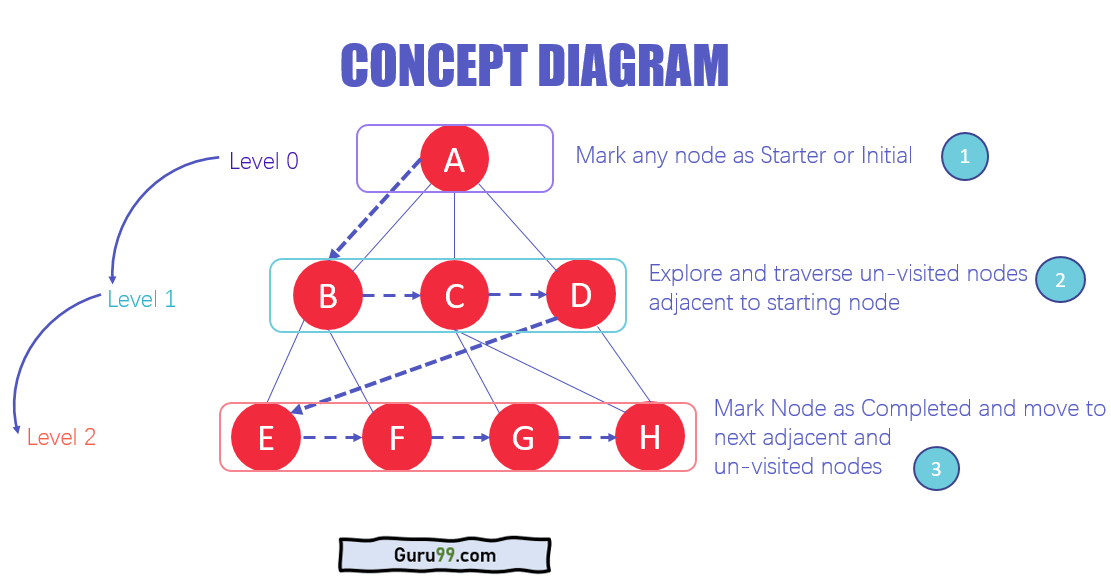
1. În diferitele niveluri ale datelor, puteți marca orice nod ca pornire sau nod inițial pentru a începe traversarea. BFS va vizita nodul și îl va marca ca vizitat și îl plasează în coadă.
2. Acum BFS va vizita nodurile cele mai apropiate și nevizitate și le va marca. Aceste valori sunt adăugate și la coadă. Coada funcționează pe modelul FIFO.
3. În mod similar, nodurile rămase cele mai apropiate și nevizitate din grafic sunt analizate marcate și adăugate la coadă. Aceste elemente sunt șterse din coadă ca primire și tipărite ca rezultat.

De ce avem nevoie de algoritmul BFS?

Există numeroase motive pentru a utiliza algoritmul BFS pe care să îl folosiți ca căutare a setului de date. Unele dintre cele mai vitale aspecte care fac din acest algoritm prima alegere sunt:

• BFS este util pentru analiza nodurilor într-un grafic și construirea celei mai scurte căi de parcurgere prin acestea.
• BFS poate parcurge un grafic în cel mai mic număr de iterații.
• Arhitectura algoritmului BFS este simplă și robustă.
• Rezultatul algoritmului BFS deține un nivel ridicat de precizie în comparație cu alți algoritmi.
• Iterațiile BFS sunt perfecte și nu există nicio posibilitate ca acest algoritm să fie prins într-o problemă de buclă infinită.

Cum funcționează algoritmul BFS?

Trecerea graficului necesită algoritmul pentru a vizita, verifica și / sau actualiza fiecare nod nevizitat într-o structură asemănătoare copacului. Traversările graficului sunt clasificate după ordinea în care vizitează nodurile din grafic.

Algoritmul BFS începe operațiunea de la primul nod sau de la început într-un grafic și îl parcurge temeinic. Odată ce traversează cu succes nodul inițial, atunci următorul vârf ne-traversat din grafic este vizitat și marcat.

Prin urmare, puteți spune că toate nodurile adiacente vârfului curent sunt vizitate și traversate în prima iterație. O metodologie simplă de coadă este utilizată pentru a implementa funcționarea unui algoritm BFS și constă din pașii următori:

Pasul 1)

Fiecare vârf sau nod din grafic este cunoscut. De exemplu, puteți marca nodul ca V.

Pasul 2)

În cazul în care vârful V nu este accesat, adăugați vârful V în coada BFS

Pasul 3)

Porniți căutarea BFS și, după finalizare, marcați vârful V ca vizitat.

Pasul 4)

Coada BFS este încă nu este gol, deci eliminați vârful V al graficului din coadă.

Pasul 5)

Recuperați toate vârfurile rămase pe graficul adiacent vârfului V

Pasul 6)

Pentru fiecare vârf adiacent, să spunem V1, în cazul în care nu este vizitat încă, adăugați V1 la coada BFS

Pasul 7)

BFS va vizita V1 și îl va marca ca vizitat și îl va șterge din coadă.

Exemplu de algoritm BFS

Pasul 1)

Aveți un grafic de șapte numere cuprinse între 0 – 6.

Pasul 2)

0 sau zero a fost marcat ca nod rădăcină.

Pasul 3)

0 este vizitat, marcat și inserat în structura datelor cozii.

Pasul 4)

Restul de 0 noduri adiacente și nevizitate sunt vizitate, marcate și inserate în coadă.

Pasul 5)

Iterațiile de traversare se repetă până când toate nodurile sunt vizitate.

Regulile algoritmului BFS

Aici sunt reguli importante pentru utilizarea algoritmului BFS:

• Structura de date a unei cozi (FIFO-First in First Out) este folosit de BFS.
• Marcați orice nod din grafic ca rădăcină și începeți să parcurgeți datele din acesta.
• BFS parcurge toate nodurile din grafic și le lasă în continuare ca terminate.
• BFS vizitează un nod adiacent nevizitat, îl marchează ca terminat și îl introduce într-o coadă.
• Elimină vârful anterior din coadă în cazul în care nu este găsit niciun vârf adiacent.
• Algoritmul BFS iterează până când toate vârfurile din grafic sunt parcurse cu succes și marcate ca finalizate.
• Nu există bucle cauzate de BFS în timpul traversării datelor de la vreun nod.

Aplicații ale algoritmului BFS

Să luăm o uitați-vă la unele dintre aplicațiile din viața reală în care o implementare a algoritmului BFS poate fi extrem de eficientă.

• Grafice neponderate: algoritmul BFS poate crea cu ușurință cea mai scurtă cale și un copac minim care să viziteze toate vârfurile graficului în cel mai scurt timp posibil cu precizie ridicată.
• Rețele P2P: BFS poate fi implementat pentru a localiza toate nodurile cele mai apropiate sau învecinate într-o rețea de la egal la egal. Aceasta va găsi datele necesare mai repede .
• Web Crawlers: motoarele de căutare sau crawlerele web pot construi cu ușurință mai multe niveluri de indexuri utilizând BFS. Implementarea BFS începe de la sursă, care este pagina web, și apoi vizitează toate linkurile din acea sursă. .
• Sisteme de navigație: BFS vă poate ajuta să găsiți toate locațiile învecinate din locația principală sau sursă.
• Difuzare în rețea ing: Un pachet difuzat este ghidat de algoritmul BFS pentru a găsi și a ajunge la toate nodurile pentru care are adresa.

Rezumat

• O traversare a graficului este un proces unic care necesită algoritmul pentru a vizita, verifica și / sau actualiza fiecare nod nevizitat dintr-un structură asemănătoare copacului. Algoritmul BFS funcționează pe un principiu similar.
• Algoritmul este util pentru analiza nodurilor dintr-un grafic și construirea celei mai scurte căi de parcurgere prin acestea.
• Algoritmul parcurge graficul în cel mai mic număr de iterații și în cel mai scurt timp posibil.
• BFS selectează un singur nod (punct inițial sau sursă) într-un grafic și apoi vizitează toate nodurile adiacente nodului selectat. BFS accesează aceste noduri unul câte unul.
• Datele vizitate și marcate sunt plasate într-o coadă de către BFS. O coadă funcționează pe baza primului în primul în primul ieșit. Prin urmare, elementul plasat mai întâi în grafic este șters mai întâi și tipărit ca rezultat.
• Algoritmul BFS nu poate fi niciodată prins într-o buclă infinită.
• Datorită preciziei ridicate și implementării robuste, BFS este utilizat în mai multe soluții din viața reală, cum ar fi rețelele P2P, Web Crawlers, și difuzarea în rețea.