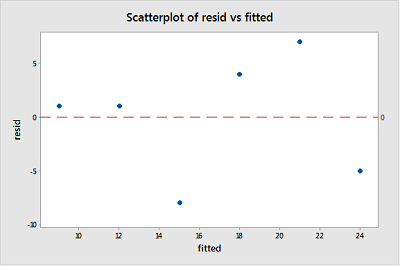
Atunci când se efectuează o analiză reziduală, un „diagramă reziduală versus potriviri” este diagrama cea mai frecvent creată. Este un grafic dispersat de reziduuri pe axa y și valori ajustate (răspunsuri estimate) pe axa x. Complotul este folosit pentru a detecta non-liniaritatea, variațiile de eroare inegale și valorile aberante.
Să vedem un exemplu pentru a vedea cum arată un grafic rezidual „bine comportat”. Unii cercetători (Urbano- Marquez, și colab., 1989) au fost interesați să stabilească dacă consumul de alcool a fost sau nu legat în mod liniar de forța musculară. Cercetătorii au măsurat consumul total de alcool pe viață (x) pe un eșantion aleatoriu de n = 50 bărbați alcoolici. puterea (y) mușchiului deltoid din brațul nedominant al fiecărei persoane. O linie grafică potrivită a datelor rezultate, (alcoholarm.txt), arată ca:
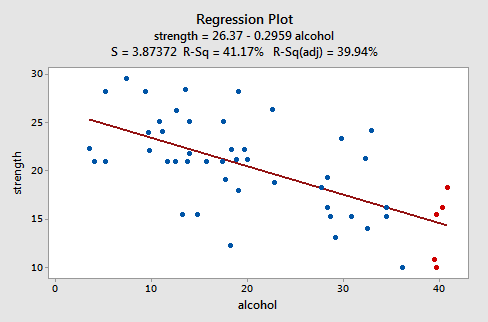
Complotul sugerează că există o relație liniară în scădere între alcool și tăria brațului. De asemenea, sugerează că nu există puncte de date neobișnuite în setul de date. Și, ilustrează faptul că variația în jurul liniei de regresie estimată este constantă, sugerând că presupunerea unor varianțe de eroare egale este rezonabilă.
Iată „cum arată graficul de reziduuri corespunzătoare versus potriviri pentru setul de date” model de regresie liniară simplă cu puterea brațului ca răspuns și nivelul consumului de alcool ca predictor:
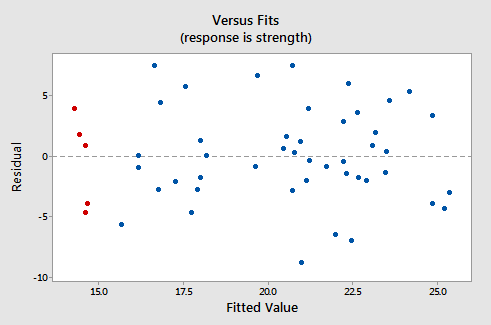
Rețineți că, așa cum este definit, reziduurile apar pe axa y, iar valorile ajustate apar pe axa x. Ar trebui să puteți privi înapoi la graficul de dispersie al datelor și să vedeți cum punctele de date de acolo corespund punctelor de date din graficul rezidual față de potriviri aici. În cazul în care aveți probleme cu acest lucru, uitați-vă la cele cinci puncte de date din graficul de împrăștiere original care apar în roșu. Rețineți că răspunsul prezis (valoarea ajustată) a acestor bărbați (al căror consum de alcool este de aproximativ 40) este de aproximativ 14 De asemenea, rețineți modelul în care cele cinci puncte de date se abat de la linia de regresie estimată.
Acum uitați-vă cum și unde aceste cinci puncte de date apar în graficul reziduale versus ajustări. Valoarea lor ajustată este de aproximativ 14 iar abaterea lor de la linia reziduală = 0 împărtășește același model ca abaterea lor de la linia de regresie estimată. Vedeți conexiunea? Orice punct de date care cade direct pe linia de regresie estimată are un reziduu de 0. Prin urmare, Linia 0 corespunde liniei de regresie estimate.
Acest grafic este un exemplu clasic al unui grafic rezidual bine-comparat față de potriviri. Iată caracteristicile unui grafic rezidual vs. sugerează oportunitatea simplului Modelul de regresie liniară:
- Reziduurile „săresc aleator” în jurul liniei 0. Acest lucru sugerează că presupunerea că relația este liniară este rezonabilă.
- Reziduurile formează aproximativ o „bandă orizontală” în jurul liniei 0. Acest lucru sugerează că varianțele termenilor de eroare sunt egale.
- Niciun reziduu „nu iese în evidență” de tiparul de bază aleatoriu al reziduurilor. Acest lucru sugerează că nu există valori aberante.
În general, doriți ca parcelele dvs. reziduale vs. Nu uitați însă că interpretarea acestor comploturi este subiectivă. Experiența mea a fost că elevii care învață analiza reziduală pentru prima dată tind să interpreteze în exces aceste comploturi, luând în considerare fiecare întorsătură ca ceva potențial supărător. Veți dori mai ales să aveți grijă să puneți prea multă greutate pe graficele reziduale vs. Uneori, seturile de date sunt prea mici pentru a face utilă interpretarea unui complot rezidual vs. Nu vă faceți griji! Veți învăța – cu practică – cum să „citiți” aceste grafice.