1.3: Efectul Bernoulli

Să presupunem că aerul este pompat pe un tub rotund neted, care are un diametru constant, cu excepția unei secțiuni din mijloc unde tubul se îngustează până la jumătate din diametru, apoi se lărgește din nou. Să presupunem că toate schimbările de diametru au loc fără probleme, iar aerul curge constant pe tub, fără turbulențe sau turbulențe.

Pentru a vedea cum ar putea fi acest lucru, vom aplica tehnicile pe care le-am dezvoltat pentru a afla cum variază presiunea într-un fluid staționar. Amintiți-vă modul în care am făcut asta a fost prin desenarea unei diagrame a corpului liber pentru un cilindru mic de fluid. Deoarece acest cilindru mic a fost în repaus, forța totală asupra acestuia a fost zero, astfel încât presiunea netă a echilibrat greutatea. Acum ia în considerare un fluid în mișcare constantă. Este util să vizualizați fluxul trasând linii aerodinamice, linii astfel încât direcția lor să fie direcția în care fluidul se mișcă în fiecare punct.

De fapt, aceste linii aeriene nu numai că îți spun direcția în care se mișcă fluidul, dar oferă și o idee despre viteza – în cazul în care se apropie, fluidul trebuie să se deplaseze mai repede, deoarece circulă aceeași cantitate de fluid printr-o regiune mai îngustă. Imaginați-vă acum un cilindru de aer care se mișcă de-a lungul conductei, axa sa fiind paralelă cu linia de curgere. Evident, trebuie să accelereze când intră în partea îngustă a tubului – deoarece aceeași cantitate de aer curge prin partea îngustă ca și partea largă, trebuie să meargă mai repede.

Dar dacă micul cilindrul de fluid se accelerează, acesta trebuie acționat de o forță care îl împinge din spate.

Greutatea sa este irelevantă aici, deoarece se mișcă orizontal. Prin urmare, singura forță care acționează asupra sa este presiunea și trebuie să concluzionăm că presiunea din spatele său este mai mare decât presiunea din față. Prin urmare, presiunea trebuie să scadă la intrarea în partea îngustă. Pentru a clarifica ce se întâmplă, vom desena un cilindru destul de mare:

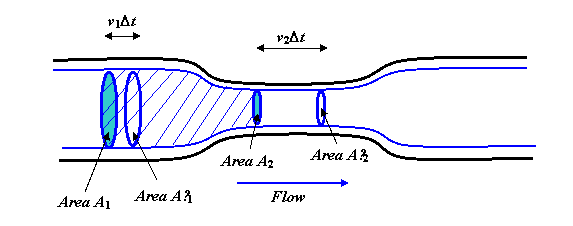
Fluidul curge constant și lin Conducta. Liniile albastre groase sunt linii aerodinamice, de fapt, ar trebui să vă imaginați că rotiți întreaga diagramă în jurul axei centrale pentru a obține o imagine tridimensională, iar liniile albastre ar deveni un cilindru, cu o secțiune „gât” mai îngustă, ecou formei țeavă.

Acum, luați în considerare corpul fluidului în interiorul liniilor de curent prezentate și acoperit la cele două capete de zonele circulare A1 și A2. Rata de curgere a fluidului pe A1 trebuie să fie aceeași cu rata de curge peste A2, deoarece în flux constant fluidul nu poate fi acumulat în mijloc (sau să se epuizeze de acolo). Volumul care curge pe A1 într-o secundă este v1A1. (Pentru a vedea acest lucru, imaginați-vă o conductă lungă dreaptă, fără o îngustă parte. Dacă fluidul curge, să zicem 3 metri pe secundă, atunci într-o secundă tot fluidul care se afla la 3 metri de zona A1 de pe partea amonte va fi trecut prin.)

Deci, fluxul peste A1 este egal cu fluxul prin A2, \

(Notă de subsol: Poate merită menționat faptul că presupunem implicit viteza ty este același în toate punctele zonei A1. Orice fluid real are o anumită vâscozitate (frecare) și se va deplasa mai încet lângă părțile laterale ale țevii decât în mijloc. Vom discuta despre asta mai târziu. Deocamdată, considerăm un fluid „ideal”, termenul folosit atunci când cineva ignoră vâscozitatea. De fapt, rezultatul pe care îl obținem este ok – am fi putut lua o mică zonă A1 departe de laturi, astfel încât viteza ar fi fost la fel pentru întreaga zonă, dar asta ar fi dat o diagramă mult mai puțin clară.)

Acum suntem pregătiți să examinăm creșterea energiei cinetice a fluidului pe măsură ce se accelerează în partea îngustă, și înțelegeți cum diferența de presiune a făcut lucrarea necesară pentru a o accelera.

\

Singura sursă posibilă pentru această creștere a energiei este munca făcută prin presiune în împingerea fluidului în partea îngustă.

\

Deci, aceasta este lucrarea făcută pe bucata noastră de fluid prin fluidul care îl împinge din spate – dar nu acesta este sfârșitul poveștii, deoarece bucata noastră de fluidul în sine funcționează împingând fluidul în fața acestuia, așa că, pentru a găsi creșterea totală a energiei bucății noastre, trebuie să scădem lucrarea externă pe care o face.Adică, munca totală efectuată prin presiunea asupra fluidului nostru este

\

amintindu-ne că \ (A_1v_1 = A_2v_2 \).

Această muncă realizată trebuie să fie egală schimbarea energiei cinetice, deci

\

din care

\

Aceasta este ecuația lui Bernoulli.

\.