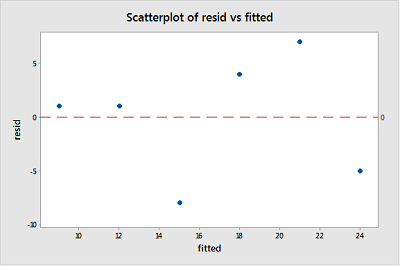
残差分析を実行する場合、「残余vs適合プロット」が最も頻繁に作成されるプロットです。これは、y軸の残差と、x軸の近似値(推定応答)の散布図です。プロットは、非線形性、不均等な誤差分散、および外れ値を検出するために使用されます。
例を見て、「行儀の良い」残差プロットがどのように見えるかを見てみましょう。一部の研究者(Urbano- Marquez、et al。、1989)は、アルコール消費量が筋力に直線的に関連しているかどうかを判断することに関心がありました。研究者は、n = 50人のアルコール男性のランダムサンプルでアルコールの全生涯消費量(x)を測定しました。各人の非利き腕のデルトイド筋の強さ(y)。結果のデータ(alcoholarm.txt)の近似折れ線グラフは、次のようになります。
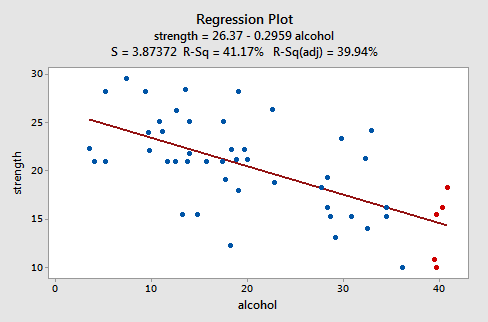
プロットは、アルコールと腕の強さの間に線形関係が減少していることを示唆しています。また、データセットに異常なデータポイントがないことも示しています。また、推定された回帰直線の周りの変動が一定であることを示しています。これは、等しい誤差分散の仮定が妥当であることを示しています。
これは、データセットの対応する残差対適合プロットがどのように見えるかを示しています。応答として腕の強さを、予測因子としてアルコール消費のレベルを使用した単純な線形回帰モデル:
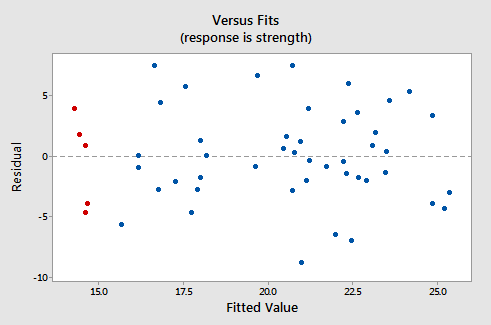
定義されているように、残差はy軸に表示され、近似値はx軸に表示されることに注意してください。データの散布図を振り返り、そこにあるデータポイントが残余対近似プロットのデータポイントにどのように対応しているかを確認できるはずです。それがうまくいかない場合は、元の散布図の赤で表示されている5つのデータポイントを見てください。これらの男性(アルコール消費量が約40)の予測応答(適合値)は約14であることに注意してください。 。また、5つのデータポイントが推定された回帰直線から逸脱するパターンに注意してください。
ここで、これらの5つのデータポイントが残差対適合プロットのどこにどのように表示されるかを見てください。それらの適合値は約14です。残差= 0の線からの偏差は、推定された回帰線からの偏差と同じパターンを共有します。接続がわかりますか?推定された回帰線に直接当たるデータポイントの残差は0です。したがって、残差= 0の線は、推定された回帰線に対応します。
このプロットは、正常に動作する残差と近似のプロットの古典的な例です。これは、正常に動作する残差と近似のプロットの特性とその特徴です。単純化の適切性について提案するe線形回帰モデル:
- 残差は0ラインの周りで「ランダムに跳ね返ります」。これは、関係が線形であるという仮定が妥当であることを示唆しています。
- 残差は、0線の周りに大まかに「水平バンド」を形成します。これは、誤差項の分散が等しいことを示しています。
- 残差の基本的なランダムパターンから「目立つ」残差はありません。これは、外れ値がないことを示しています。
一般に、残差対適合プロットは上記のプロットのようになります。これらのプロットの解釈は主観的であることを忘れないでください。私の経験では、残余分析を初めて学ぶ学生は、これらのプロットを過度に解釈し、あらゆるねじれや方向転換を潜在的に厄介なものと見なす傾向があります。小さなデータセットに基づく残差対近似プロットに過度の重みをかけることに注意してください。データセットが小さすぎて、残差と近似のプロットを解釈する価値がない場合があります。心配しないでください。これらのプロットを「読み取る」方法を練習で学びます。